
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Екі белгісізді екі және үш белгісізді үш теңдеулер жүйесі
|
|
Анықтама 1Екі белгісізді екі теңдеулер жүйесі деп
 |
(1)
сызықты теңдеулер жүйесін айтамыз.
Мұндағы 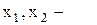 белгісіз шамалар,
белгісіз шамалар,  - і нөмірлі теңдеудегі j нөмірлі белгісіздің коэффициенті
- і нөмірлі теңдеудегі j нөмірлі белгісіздің коэффициенті 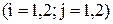 ,
,  і нөмірлі теңдеудің бос мүшесі.
і нөмірлі теңдеудің бос мүшесі.
Мысалы,  - екінші теңдеудегі
- екінші теңдеудегі 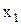 - дің коэффициенті,
- дің коэффициенті, 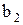 - осы теңдеудегі бос мүше.
- осы теңдеудегі бос мүше.
Анықтама 2 Егер белгісіздердің  мәндері
мәндері 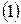 жүйесіндегі екі теңдеуді де қанағаттандырса, онда осы сандар жүйенің шешімі деп аталады және
жүйесіндегі екі теңдеуді де қанағаттандырса, онда осы сандар жүйенің шешімі деп аталады және  деп белгіленеді.
деп белгіленеді.
Анықтама 3 Егер 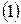 сызықты теңдеулер жүйесінің ең кемінде бір шешімі бар болса, онда бұл жүйе үйлесімді, ал бірде бір шешімі болмаса үйлесімсіз деп аталады. Егер үйлесімді жүйенің тек қана бір шешімі бар болса, онда бұл жүйе анықталған, ал кемінде екі шешімі бар болса, онда анықталмаған деп аталады.
сызықты теңдеулер жүйесінің ең кемінде бір шешімі бар болса, онда бұл жүйе үйлесімді, ал бірде бір шешімі болмаса үйлесімсіз деп аталады. Егер үйлесімді жүйенің тек қана бір шешімі бар болса, онда бұл жүйе анықталған, ал кемінде екі шешімі бар болса, онда анықталмаған деп аталады.
 ,
, 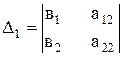 ,
, 
деп алайық.  берілген теңдеулер жүйесінің анықтауышы деп аталады.
берілген теңдеулер жүйесінің анықтауышы деп аталады.  -осы анықтауыштың бірінші тік жолын, ал
-осы анықтауыштың бірінші тік жолын, ал  -екінші тік жолын бос мүшелермен алмастыру арқылы жасалған анықтауыштар.
-екінші тік жолын бос мүшелермен алмастыру арқылы жасалған анықтауыштар.
Негізгі тұжырымдар: 1) Егер  болса, онда берілген жүйе үйлесімді анықталған, ал
болса, онда берілген жүйе үйлесімді анықталған, ал 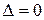 болып
болып  мен
мен  -нің ең кемінде біреуі нөлге тең болмаса, онда бұл жүйе үйлесімсіз болады; 2) Егер
-нің ең кемінде біреуі нөлге тең болмаса, онда бұл жүйе үйлесімсіз болады; 2) Егер  коэффициенттерінің ең кемінде біреуі нөлге тең болмай
коэффициенттерінің ең кемінде біреуі нөлге тең болмай 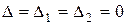 болса, онда берілген жүйе анықталмаған үйлесімді жүйе. Мұндай жүйенің бір параметрден тәуелді шексіз көп шешімі бар болады.
болса, онда берілген жүйе анықталмаған үйлесімді жүйе. Мұндай жүйенің бір параметрден тәуелді шексіз көп шешімі бар болады.
Крамер әдісі: Анықталған жүйенің шешімі

формулалары арқылы анықталады
Анықтама 4 Үш белгісізді үш теңдеулержүйесі деп
 (2)
(2)
сызықтық теңдеулер жүйесін айтамыз.
Мұндағы 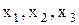 белгісіз шамалар,
белгісіз шамалар,  -
- 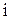 нөмерлі теңдеудегі
нөмерлі теңдеудегі 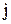 нөмерлі белгісіздің коэффициенті
нөмерлі белгісіздің коэффициенті  ,
, 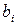 -
- 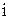 нөмірлі теңдеудің бос мүшесі. Бұл жүйе үйлесімді немесі үйлесімсіз болуы мүмкін. Үйлесімді жүйе анықталған немесе анықталмаған болады.
нөмірлі теңдеудің бос мүшесі. Бұл жүйе үйлесімді немесі үйлесімсіз болуы мүмкін. Үйлесімді жүйе анықталған немесе анықталмаған болады.
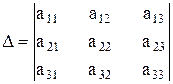 ,
, 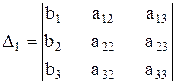 ,
,
 ,
, 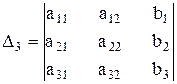
деп алайық, мұндағы  -берілген жүйенің анықтауышы,
-берілген жүйенің анықтауышы,  -осы анықтауыштың k-нөмірлі тік жолын бос мүшелермен алмастыру арқылы жасалған анықтауыштар.
-осы анықтауыштың k-нөмірлі тік жолын бос мүшелермен алмастыру арқылы жасалған анықтауыштар.
Негізгі тұжырымдар: 1) Егер  болса, онда
болса, онда 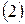 үйлесімді анықталған жүйе, ал
үйлесімді анықталған жүйе, ал 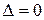 болып
болып  анықтауыштарының ең кемінде біреуі нөлге тең болмаса, онда
анықтауыштарының ең кемінде біреуі нөлге тең болмаса, онда 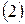 үйлесімсіз жүйе;
үйлесімсіз жүйе;
2) Егер 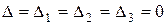 болып,
болып,  анықтауышының элементтерінен тік және жатық жолдарының реттерін сақтап жасалған, нөлге тең болмайтын екінші ретті анықтауыш бар болса, онда
анықтауышының элементтерінен тік және жатық жолдарының реттерін сақтап жасалған, нөлге тең болмайтын екінші ретті анықтауыш бар болса, онда 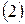 үйлесімді анықталмаған жүйе. Мұндай жүйенің бір параметрден тәуелді шексіз көп шешімі бар болады; 3) Егер
үйлесімді анықталмаған жүйе. Мұндай жүйенің бір параметрден тәуелді шексіз көп шешімі бар болады; 3) Егер  коэффициентерінің ең кемінде біреуі нөлге тең болмаса,
коэффициентерінің ең кемінде біреуі нөлге тең болмаса,  анықтауышының элементтері мен бос мүшелерінен тік және жатық жолдарының реттерін сақтап, жасалған барлық екінші ретті анықтауыштар нөлге тең болса, онда
анықтауышының элементтері мен бос мүшелерінен тік және жатық жолдарының реттерін сақтап, жасалған барлық екінші ретті анықтауыштар нөлге тең болса, онда 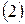 үйлесімді анықталмаған жүйе. Бұл жүйенің екі параметрге тәуелді шексіз көп шешімдері бар болады.
үйлесімді анықталмаған жүйе. Бұл жүйенің екі параметрге тәуелді шексіз көп шешімдері бар болады.
Крамер әдісі: Анықталған жүйенің шешімі


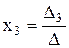
формулалары арқылы анықталады. Бұл формулалар Крамер формулалары деп аталады.
Өздік жұмысы
1. 
| 2. 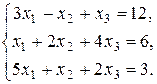
|
3. 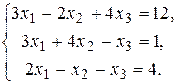
|
4. 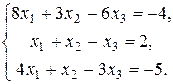
|
5. 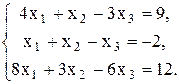
|
6. 
|
7. 
|
8. 
|
9. 
|
10. 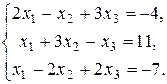
|
11. 
| 12. 
|
13. 
|
14. 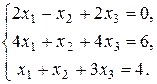
|
15. 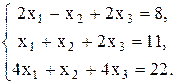
| 16. 
|
17. 
|
18. 
|
19. 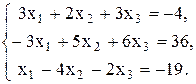
|
20. 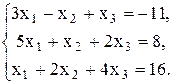
|
21. 
|
22. 
|
23. 
|
24. 
|
25. 
| 26. 
|
27. 
|
28. 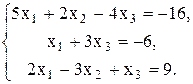
|
29. 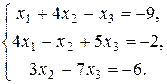
|
30. 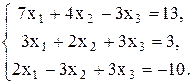
|
23.09
Date: 2016-06-09; view: 1775; Нарушение авторских прав