
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Аналитическое выравнивание по прямой
|
|
В динамическом ряду со стабильными абсолютными приростами выравнивание производится по функции прямой:  , где t – время;
, где t – время;  - уровень тренд;
- уровень тренд;  - параметры уравнения;
- параметры уравнения;  - коэффициент регрессии, определяет направление развития;
- коэффициент регрессии, определяет направление развития;
 : рост уровней ряда в среднем на эту величину (равномерный)
: рост уровней ряда в среднем на эту величину (равномерный)
 : снижение уровней ряда в среднем на эту величину (равномерное).
: снижение уровней ряда в среднем на эту величину (равномерное).
Для вычисления параметров функции с помощью метода метода наименьших квадратов составляется система нормальных уравнений:
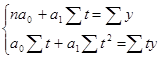 è
è 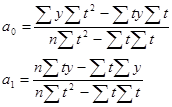
Таблица 3.
Динамика товарооборота области за 1990-1995 гг.
| Годы | Объём товарооборота, млн.руб. | Абсолютный прирост (цепной), млн. руб. |
| 11,18 12,23 13,28 14,31 15,36 16,40 | – 1,05 1,05 1,03 1,05 1,04 | |
| В среднем: | 14,32 | 1,04 |
Здесь абсолютные приросты относительно стабильны.
Таблица 4.
Матрица расчётных показателей.
| Годы | Объём товарооборота, млн. руб. | 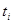
| 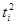
| 
| 
|
| 11,18 12,23 13,28 14,31 15,36 16,40 | 11,18 24,46 39,84 57,24 76,80 98,40 | 11,183 12,226 13,269 14,312 15,355 16,398 | |||
| Всего: | 82,76 | 307,92 | 82,743 |

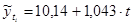
 , т.е. объём товарооборота в среднем ежегодно возрастал на 1,043 млн. руб.
, т.е. объём товарооборота в среднем ежегодно возрастал на 1,043 млн. руб.
Можно составить прогноз:
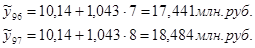
Адекватность математической функции проверяется через расчёт стандартизованной ошибки аппроксимации. За наиболее адекватную принимается модель (функция),у которой ошибка аппроксимации минимальна.
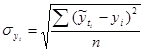
По окончании расчёта основной тенденции рекомендуется построить график, на котором следует изобразить фактические (эмпирические) и теоретические значения уровней ряда.
Для определения параметров математических функций при анализе тренда в рядах динамики можно использовать способ отсчёта времени от условного начала, когда показатель времени t обозначают таким образом, чтобы ∑t=0. В ряду динамики с нечётным числом уровней порядковый номер находящегося в середине ряда уровня обозначается как “0” (условное начало отсчёта времени), показатели времени всех предыдущих уровней обозначаются с интервалом (-1), а всех последующих – с интервалом (+1) (например, при n=5 t будут: -2,-1,0,+1,+2). При чётном числе уровней (например, n=6), порядковые номера верхней половины ряда (от середины) обозначатся числами (сверху вниз): -5, -3, -1, а нижней половины: +1,+3,+5.
9.6. Экстраполяция и интерполяция.
Статистическая оценка возможностей развития социально-экономических явлений является важным условием регулирования рыночных отношений.
Экстраполяция – это нахождение значений функции за пределами её области определения на основе информации о поведении функции в области определения. При изучении рядов динамики это продолжение уровней ряда динамики в будущее (перспективная экстраполяция) или в прошлое (ретроспективная экстраполяция) на основе выявленной закономерности измерения уровней в изучаемом отрезке времени.
Интерполяция – это нахождение промежуточных значений функции в области её определения, т.е. в рядах динамики – для нахождения промежуточных уровней временного ряда.
Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики как базы прогнозирования, сохраняется в дальнейшем.
Важное значение при экстраполяции имеет продолжительность базисного ряда динамики и сроки прогнозирования.
Правильнее брать для экстраполяции часть ряда динамики субпериод, который является определённым этапом в развитии явления в конкретных исторических условиях. Кроме того, ем короче сроки упреждения прогноза, тем надёжнее результаты экстраполяции.
Методы экстраполяции применяются в зависимости от характера изменений в ряду динамики и задач исследования.
1) При экстраполяции на базе рядов динамики с постоянными абсолютными приростами (аналитическое выравнивание по уравнению прямой) применяется формула:
 (1), где
(1), где  - прогнозируемый уровень,
- прогнозируемый уровень, 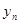 - конечный уровень базисного ряда,
- конечный уровень базисного ряда, 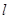 - срок прогноза.
- срок прогноза.
2) При экстраполяции на базе рядов динамики со стабильными темпами роста (выравнивание по уравнению показательной функции)
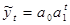 (2), где
(2), где  - темп роста (снижения) в единицу времени.
- темп роста (снижения) в единицу времени.
применяется формула:
 (3).
(3).
В результате применения формул (1) и (3) получается точечная (дискретная) оценка. На практике экстраполяция чаще осуществляется интервальными оценками. Для определения границ интервалов используется формула:
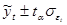 (4), где
(4), где  - коэффициент доверия по распределению Стьюдента,
- коэффициент доверия по распределению Стьюдента, 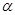 - уровень значимости по таблице.
- уровень значимости по таблице.
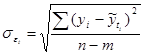 (5) - это остаточное среднее квадратическое отклонение тренда, скорректированное по числу степеней свободы (n-m). n – число уровней базисного ряда динамики, m – число параметров модели тренда.
(5) - это остаточное среднее квадратическое отклонение тренда, скорректированное по числу степеней свободы (n-m). n – число уровней базисного ряда динамики, m – число параметров модели тренда.
Полученный по (2) прогноз  конкретного периода корректируется на величину интервала (
конкретного периода корректируется на величину интервала (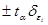 ), т.е. прогнозируемая на конкретный год величина явления будет иметь верхнюю и нижнюю границу.
), т.е. прогнозируемая на конкретный год величина явления будет иметь верхнюю и нижнюю границу.
9.7. Изучение сезонных колебаний.
Под сезонными колебаниями понимаются более/менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений (из месяца в месяц, их квартала в квартал). Ярко выраженный сезонный характер имеет сельскохозяйственное производство, туризм, спрос на ТНП в зависимости от периода времени (года). Анализ сезонных колебаний особенно необходим в маркетинговых исследованиях, когда выявляется соотношение спроса и предложения на конкретные товары и услуги и т.п.
При изучении внутригодовой динамики сезонных колебаний статистика решает две задачи:
1) выявить специфику развития явления во внутригодовой динамике;
2) измерить сезонные колебания с помощью построения модели сезонной волны.
1) Ряды внутригодовой динамики составляется по материалам текущей отчётности. Обязательно их надо привести к сопоставимому виду (сомкнуть, пересчитать в сопоставимые цены или по единой методике). Если периоды времени (месяц, квартал) разные поп продолжительности (30 дней и 31 день), то фактические величины пересчитываются в средние величины, характеризующие развитие явления в единицу времени (в день, т.е. среднедневные).
2) Для измерения сезонных колебаний исчисляются индивидуальные индексы сезонности (1)  , где
, где 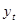 - исходные уровни ряда динамики,
- исходные уровни ряда динамики,  - расчётные (выравненные) уровни ряда динамики (по тренду).
- расчётные (выравненные) уровни ряда динамики (по тренду).
В (1) устраняется влияние основной тенденции на сезонные колебания. Для устранения случайных отклонений производится усреднение индивидуальных индексов is одноимённых периодов (месяцев, кварталов) ряда динамики.
Для каждого периода определяются средние индексы сезонности:
(2) 
В зависимости от характера тренда применяются следующие формы среднего индекса сезонности:
а) если в ряду динамики основная тенденция ярко выражена (т.е. рост или снижение постоянны):
(3) 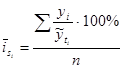 - способ переменной средней.
- способ переменной средней.
б) если в ряду динамики отсутствует чёткий рост (снижение) уровней или он незначителен:
(4) 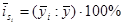 - способ постоянной средней, где
- способ постоянной средней, где 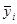 - средний уровень периода i,
- средний уровень периода i, 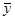 - общая средняя.
- общая средняя.
Этапы исследования сезонных колебаний:
1) фактические ряды динамки приводятся к сопоставимому виду;
2) производится расчёт показателей динамики (абсолютный прирост, темпы роста, темпы прироста) и определяется тенденция ряда к росту (снижению) или её отсутствие и, следовательно, способ расчёта индекса сезонности: способ переменной средней или способ постоянной средней;
3) подбирается математическая функция, по которой будет производиться аналитическое выравнивание и определяться теоретические (расчётные) уровни ( ). Обычно выбирается несколько математических функций (прямая, парабола, гипербола и т.п.); оптимальная определяется по минимальному уровню ошибки аппроксимации;
). Обычно выбирается несколько математических функций (прямая, парабола, гипербола и т.п.); оптимальная определяется по минимальному уровню ошибки аппроксимации;
4) рассчитываются теоретические уровни ряда динамики; потом индивидуальные индексы сезонности для каждого периода;
5) рассчитываются средние индексы сезонности по способу, выбранному в п.2.
6) строится график (сезонная волна) роста (снижения) объёмного показателя.
Для выявления сезонных колебаний можно применять метод скользящей средней.
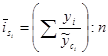 , где
, где 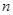 - число одноимённых периодов,
- число одноимённых периодов,  - уровни рядов динамики, сглаженные по средней.
- уровни рядов динамики, сглаженные по средней.
Тема 10. Индексный метод.
10.1. Понятие и классификация индексов.
10.2. Агрегатные индексы. Система индексов.
10.3. Средние индексы.
10.4. Цепные и базисные индексы.
10.5. Изучение индексным методом влияния структурных сдвигов.
10.6. Территориальные индексы.
10.1. Понятие и классификация индексов.
Наиболее широко в экономической практике и статистическом анализе при исследовании сложных социально-экономических явлений применяется индексный метод.
Статистический индекс (index - показатель) – это относительная величина сравнения сложных совокупностей и их отдельных единиц. Сложной называется статистическая совокупность, отдельные элементы которой непосредственно не поддаются суммированию (например, характеристика продукции разных видов в натурально-вещественной форме; объем товарооборота).
Основой индексного метода является переход от натурально-вещественной формы выражения сложных явлений к стоимостным измерителям.
Индексный метод позволяет решить три основные задачи статистических исследований:
1) сравнить характеристики совокупностей, состоящих из не суммируемых элементов;
2) провести факторный анализ, то есть измерить влияние различных факторов на обобщающий показатель (сложное явление);
3) проанализировать влияние структурных сдвигов, то есть изменений в структуре изучаемого сложного явления, на обобщающий показатель.
Классификация индексов.
1) В зависимости от сущностей показателей, характеризующих изучаемое явление (совокупность) индексы делятся на индексы количественных показателей (количества продукции, физического объема товарооборота, национального дохода и т. п.) и индексы качественных показателей (индексы цен, себестоимости, производительности труда и т. д.). Деление условное.
2) В зависимости от степени охвата единиц совокупности (элементов изучаемого сложного явления) индексы делятся на индивидуальные и общие.
Индивидуальные индексы характеризуют изменение во времени (или в пространстве) отдельных единиц статистической совокупности. Обозначаются "i", выражаются в коэффициентах или в процентах. Так, индивидуальный индекс цен рассчитывается по формуле: (1) 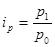 , где
, где
P1 – цена товара в текущем периоде,
P0 – цена товара в базисном периоде.
Например, изменение цены в рублях стандартной булки хлеба в текущем квартале по сравнению с предыдущим составит:
 или 123,1%, то есть цена товара выросла за рассматриваемый период на 23,1%
или 123,1%, то есть цена товара выросла за рассматриваемый период на 23,1%
Индивидуальный индекс количества проданных товаров (физического объема реализации) в натуральных единицах измерения рассчитывается по формуле:
(2) 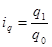 , где
, где
q1 - количество товара, реализованное в текущем периоде
q0 - количество товара, реализованное в базисном периоде
Индивидуальные индексы, характеризующие изменение явления во времени, являются, по сути, относительными показателями динамики (темпами роста), поэтому они могут рассчитываться по данным за несколько периодов времени в цепной или базисной формах.
Общие индексы (сводные) выражают обобщающие результаты изменения во времени (или в пространстве) всех единиц, образующих статистическую совокупность (сложного явления в целом). К ним относятся: общий индекс цен, общий индекс динамики товарооборота, общий индекс затрат, общий индекс продукции и т. п. Обозначаются как "I". Так общий индекс товарооборота рассчитывается по формуле:
(3) 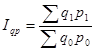 , где
, где
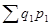 - фактический товарооборот отчетного периода
- фактический товарооборот отчетного периода
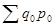 - фактический товарооборот базисного периода
- фактический товарооборот базисного периода
Разновидностью общих индексов являются групповые индексы, они охватывают часть единиц совокупности.
Каждый общий индекс имеет две составные части: индексируемая величина и веса.
Основным элементом индекса является индексируемая величина – это значение признака статистической совокупности, изменение которого является объектом изучения. Так, при изучении изменения цен индексируемой величины будет цена единицы товара "p", а весами – количество товара в натуральных единицах измерения – "q". При изучении изменения физического объема товарооборота индексируемой величиной является количество товара в натуральных измерителях – "q", а весами – цена единицы товара – "p".
По методологии расчета общие индексы делятся на агрегатные и средние из индивидуальных индексов.
10.2. Агрегатные индексы. Система индексов.
Основной формой общих индексов является агрегатная. В числителе и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых статистических совокупностей.
Веса в агрегатных индексах применяются для достижения сопоставимости разнородных единиц сложных совокупностей, то есть для перехода к однородным показателям. Для выявления влияния какого-либо конкретного фактора на индексируемую величину веса фиксируются на одном уровне (текущего или базисного периода).
Условием применения агрегатной формы индексов является наличие данных о количественных характеристиках изучаемого явления (товара, продукции и т. п.) в натуральных измерителях и данные о стоимости единицы количественного показателя.
Таблица 1.
Реализация товаров на рынке города за два периода.
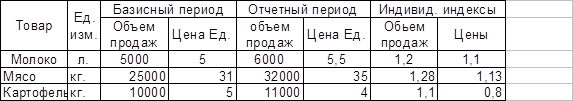
1) Рассчитаем общий индекс динамики товарооборота в фактически действовавших ценах:
(4) 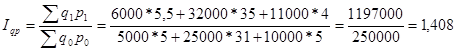 или 140,8%
или 140,8%
Данный индекс показывает, что товарооборот отчетного периода в фактически действовавших ценах вырос по сравнению с товарооборотом базисного периода на 40,8% или на 347000 рублей.
Общий прирост (снижение) явления рассчитывается как разность числителя и знаменателя данного агрегатного индекса:
 рублей, т.е.
рублей, т.е.
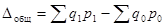
2) Агрегатный индекс физического объема товарооборота имеет вид:
(5) 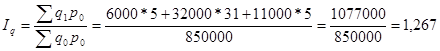 или126,7%
или126,7%
Данный индекс показывает изменение объёма товарооборота в отчетном периоде по сравнению с базисным в сопоставимых ценах, то есть ценах, зафиксированных на уровне базисного периода.
Таким образом, устраняется влияние цен и определяется рост (снижение) товарооборота вследствие изменения количества проданных товаров, в нашем примере, это рост товарооборота на 26,7% или на 227000 рублей (Абсолютный прирост, снижение определяются аналогично как с индексом Iqp)
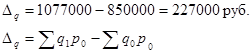
Правило: в индексах, характеризующих динамику объемов продаж и производства продукции, количества чего-либо, взвешивание производится по ценам базисного периода (прошлого), чтобы устранить влияние изменения цен на величину индекса.
3) Агрегатная форма индекса цен имеет вид:
(6) 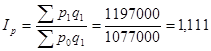 или 111,1%, называется индексом Пааше, так как был предложен немецким экономистом Г. Пааше.
или 111,1%, называется индексом Пааше, так как был предложен немецким экономистом Г. Пааше.
Этот индекс показывает изменение уровня цен по конкретной массе товаров; в данном примере, что в отчетном периоде по сравнению с базисным цены повысились в среднем на 11,1%, вследствие чего товарооборот вырос на 120000 рублей.
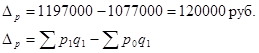
Разница между числителем и знаменателем общего индекса цен показывает абсолютное изменение (экономию или перерасход) денежных средств, потраченных на приобретение товаров населением.
Правило: в индексах качественных показателей веса берутся на уровне отчетного периода.
Существует другой способ определения агрегатного индекса цен, предложенный немецким экономистом Э. Ласпейресом:
(7) 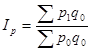 - индекс Ласпейреса.
- индекс Ласпейреса.
Индексы Пааше и Ласпейреса характеризуют различные качественные особенности изменения цен и поэтому не совпадают при расчете. Индекс Пааше характеризует влияние изменения цен на стоимость товаров, реализованных в отчетном периоде. Индекс Ласпейреса характеризует влияние изменения цен на стоимость товаров, реализованных в базисном периоде.
Индексный метод применяется для выявления и количественного определения влияния отдельных факторов на изменение сложных явлений. Для этого используются системы индексов (взаимосвязанные индексы). Чтобы образовать систему индексов, необходимо веса в разных индексах брать на уровне разных временных периодов.
Рассмотренные выше три индекса: общий индекс динамики товарооборота, общий индекс физического объема товарооборота и общий индекс цен образуют систему индексов:
(8) 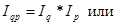
(9) 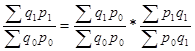
В данной системе изменение товарооборота в фактически действовавших ценах в отчетном периоде по сравнению с базисным зависит от изменения количества проданных товаров в натуральных измерителях (индекс физического объема) и от изменения цен на проданные товары (индекс цен).
Абсолютное изменение фактического товарооборота (прирост, снижение) также зависит от изменения физического объема реализации товаров в отчетном периоде по сравнению с базисным и от изменения цен за аналогичные временные периоды.
(10) 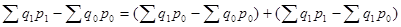
Взаимосвязанные общие индексы применяются во многих других случаях: для анализа производственной деятельности предприятий применяются индекс стоимости продукции, индекс оптовых цен и индекс физического объема продукции; для анализа затрат на производство – индекс себестоимости продукции, индекс физического объема продукции и индекс затрат на производство и т. п.
Так общий индекс затрат на производство имеет вид:
(11) 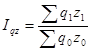 , где
, где
Z1, Z0 - себестоимость единицы продукции в текущем, базисном периоде соответственно
q1, q0 - количество произведенной продукции в текущем, базисном периоде соответственно
Общий индекс физического объема продукции рассчитывается как:
(12) 
Общий индекс себестоимости имеет вид:
(13) 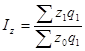
Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя покажет сумму экономии (перерасхода) предприятия от снижения себестоимости единицы продукции.
Все три индекса взаимосвязаны: 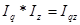 (14)
(14)
Индексный метод применяется и для анализа изменений производительности труда двумя способами:
a) через прямой показатель производительности труда (выработка) – количества продукции, выработанной в единицу времени или на одного работника (w);
b) через ее обратный показатель - трудоемкость, то есть затраты рабочего времени на производство единицы продукции (t)
Прямой и обратный показатели производительности взаимосвязаны:
(15) 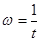
Индивидуальные индексы производительности труда имеют вид:
(16) 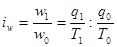 или
или
(17)  , где
, где
T1, T0 – суммарные затраты времени на выпуск данной продукции в человеко-часах, человеко-днях или человеко-месяцах (общая численность работников), соответственно, за текущий и базисный периоды.
Общий индекс производительности труда (по трудоемкости) имеет вид:
(18)  , где
, где
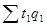 общие затраты времени на выпуск продукции в текущем периоде, то есть Т1
общие затраты времени на выпуск продукции в текущем периоде, то есть Т1
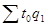 условные затраты времени на выпуск этой продукции при неизменной трудоемкости.
условные затраты времени на выпуск этой продукции при неизменной трудоемкости.
Данный индекс связан с индексом затрат рабочего времени (труда) и с индексом физического объема продукции, взвешанным по трудоемкости
(19)  или
или
(20) 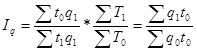
При расчете общего индекса производительности труда в стоимостном выражении (по выработке) необходимо количество продукции, произведенной за каждый период, взвесить по ценам, принятым за сопоставимые (цены текущего, базисного период, средние цены).
(21)  В данном индексе средняя выработка в текущем периоде сравнивается со средней выработкой а базисном периоде.
В данном индексе средняя выработка в текущем периоде сравнивается со средней выработкой а базисном периоде.
Умножив индекс производительности труда по выработке на индекс затрат рабочего времени получим индекс физического объема продукции, взвешенного по цене:
(22)  или
или
(23) 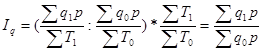
10.3. Средние индексы.
Любой общий индекс можно представить как среднюю взвешенную из индивидуальных индексов (вторая форма выражения общих индексов). При этом форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу. Применяются две формы: средняя арифметическая форма и средняя геометрическая форма (для расчета общих индексов).
1) В тех случаях когда отсутствуют данные о количестве товаров (продукции) в натуральных измерителях, но есть информация о стоимости реализованных товаров (произведенной продукции) и индивидуальные индексы изменения объемов товаров (продукции), можно определить агрегатный индекс физического объема товарооборота (продукции) по средней арифметической форме.
(24) 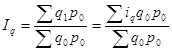 , где
, где 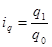
Чтобы средний арифметический индекс был тождественен агрегатному, весами индивидуальных индексов в нем должны быть взяты слагаемые знаменателя исходного агрегатного индекса.
2) В тех случаях, когда нет информации о количестве товаров (продукции) в натуральной форме, но есть учет реализации товаров (производства продукции) в стоимостном выражении и индивидуальные цены на товары (продукцию), для определения сводных показателей изменения цен применяется средняя гармоническая форма.
(25)  , где
, где 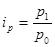
Чтобы средний гармонический индекс был тождественен агрегатному, весами индивидуальных индексов в нем должны быть взяты слагаемые числителя исходного агрегатного индекса.
10.4. Цепные и базисные индексы.
При изучении динамики социально-экономических явлений часто производятся сопоставления более чем за два периода.
- Если необходимо проанализировать изменение явления во всех последних периодах по сравнению с начальным (базовым) – вычисляются базисные индексы.
- Если требуется охарактеризовать последовательное изменение явления, из периода в период, то рассчитываются цепные индексы.
В зависимости от характера исходной информации и задач исследования можно рассчитать как индивидуальные так и общие индексы.
Индивидуальные цепные и базисные индексы рассчитываются аналогично относительным величинам динамики (темпам роста).
Общие индексы вычисляются с переменными и постоянными весами, в зависимости от их экономического содержания.
Общие индексы качественных показателей (цен, себестоимости, производительности труда) исчисляются как индексы с переменными весами (то есть весы берутся на уровне текущего – отчетного периода).
Общие индексы количественных показателей (физического объема) рассчитываются как индексы с постоянными весами, взятыми на уровне базисного (начального периода).
При этом общие цепные и базисные индексы с постоянными весами находятся во взаимосвязи:
a) Произведение цепных индексов дает базисный индекс последнего периода;
b) Деление последующего базисного индекса на предыдущий базисный индекс дает цепной индекс последующего периода.
В этих индексах весы – соизмерители взяты на уровне одного и того же базисного периода.
Общие цепные и базисные индексы с переменными весами такой взаимосвязи не имеют, так как в них весы – соизмерители берутся на уровнях разных периодов. Для всех индивидуальных индексов взаимосвязь цепных и базисных индексов сохраняется.
Таблица 2.
Данные о продаже товаров на рынке города за 4-й квартал

Индивидуальный 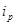
 цепные
цепные
 базисные
базисные
1,25*1,2=1,5 - сохраняется
1. Общие индексы цен:
a) цепные

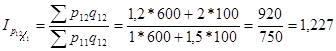
b) базисные

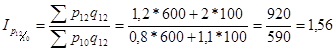
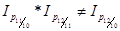
2. Общие индексы физического объема:
a) цепные
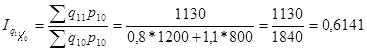
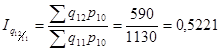
b) базисные
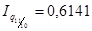
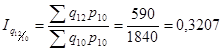
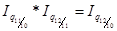
10.5. Изучение индексным методом влияния структурных сдвигов.
Взаимосвязанные индексы применяются и для изучения влияния структурных сдвигов на изменение социально-экономических явлений. В таком анализе индексы находятся во взаимосвязи со средними величинами. На среднюю величину оказывают влияние как значение усредняемого признака, так и численность отдельных вариантов, например, на среднюю цену товара влияет различие цен на этот товар на разных рынках, в магазинах и т. п., а также изменение объема реализации товара.
Для анализа влияния структурных сдвигов применяется система индексов, в которой показатель динамики средней величины (индекс переменного состава) является произведением двух индексов: индекса средней величины в неизменной структуре (индекс постоянного состава) и индекса влияния изменение структуры на динамику средней величины (индекс структурных сдвигов).
(26) 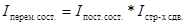
Данная система чаще всего применяется в случаях, когда один вид товара реализуется в нескольких местах или один вид продукции производится на разных предприятиях.
(27)  , где
, где
x1, x0 – значения признака (вариант), в текущем и базисном периодах, соответственно
f1, f0 – численность вариант, в текущем и базисном периодах, соответственно
(28) 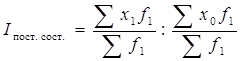 , в нем численность вариант фиксируется на уровне текущего периода (фиксируется состав), т. е. он показывает изменение непосредственное изучаемого признака.
, в нем численность вариант фиксируется на уровне текущего периода (фиксируется состав), т. е. он показывает изменение непосредственное изучаемого признака.
(29) 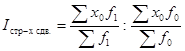 , в нем изменяются частоты, а уровень признака фиксируется по базисному периоду, т. е. он показывает влияние изменений в структуре (составе) явления на изучаемый признак.
, в нем изменяются частоты, а уровень признака фиксируется по базисному периоду, т. е. он показывает влияние изменений в структуре (составе) явления на изучаемый признак.
Следовательно, в полном виде система записывается, как
(30) 
Абсолютные изменения средних показателей также взаимосвязаны:
(31) 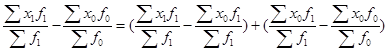 , т. е.
, т. е.
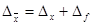
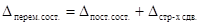
Таблица 3.
Основные показатели производственной деятельности ДСК города за 1999-2000 гг.
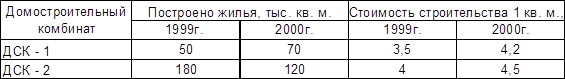
1) 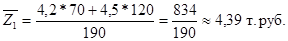
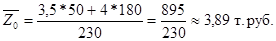
 или (112,85%), то есть в среднем стоимость строительства 1 кв. м. жилья выросла в 2000г. по сравнению с 1999г. на 12,85% или на 0,5 тыс. руб.
или (112,85%), то есть в среднем стоимость строительства 1 кв. м. жилья выросла в 2000г. по сравнению с 1999г. на 12,85% или на 0,5 тыс. руб.
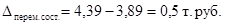
2) 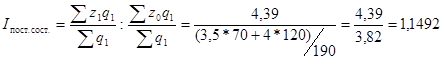 или 114,92%, то есть непосредственное изменение стоимости строительства, при условии, что структура жилья была бы на уровне 2000г., увеличило стоимость строительства 1кв. м. на 14,9% или 0,57 тыс. руб.
или 114,92%, то есть непосредственное изменение стоимости строительства, при условии, что структура жилья была бы на уровне 2000г., увеличило стоимость строительства 1кв. м. на 14,9% или 0,57 тыс. руб.

3)  или 98,2%, то есть изменение структуры строительства жилья (увеличение доли ДСК-1 и снижение доли ДСК-2 с более высокой стоимостью 1 кв. м.) повлекло за собой снижение средней стоимости строительства 1 кв. м. жилья на 1,8% или 0,07 тыс. руб.
или 98,2%, то есть изменение структуры строительства жилья (увеличение доли ДСК-1 и снижение доли ДСК-2 с более высокой стоимостью 1 кв. м.) повлекло за собой снижение средней стоимости строительства 1 кв. м. жилья на 1,8% или 0,07 тыс. руб. 
Взаимосвязь:
1,1285=1,1492*0,9820
0,5=0,57-0,07
В данной системе индексов можно выразить численные характеристики признака (вариантов) в виде удельного веса (доли) "d" (в коэффициентах).
Тогда она примет вид:
(32) 
10.6. Территориальные индексы.
Территориальные индексы служат для сравнения показателей в пространстве, то есть по предприятиям, городам, регионам и т. п.
Построение территориальных индексов определяется выбором базы сравнения и весов или уровня, на котором фиксируются веса. При двусторонних сравнениях каждая территория может быть сравниваемой (числитель индекса) и базой сравнения (знаменатель). Веса и первой и второй территории могут быть использованы при расчете индекса, но это может привести к противоречивым результатам. Поэтому предлагается два способа расчета территориальных индексов.
1) В качестве весов принимаются объемы проданных товаров (произведенной продукции) по двум вместе взятым регионам:  (33)
(33)
Территориальный индекс цен тогда имеет вид:
(34)  , где Ра, Рв – цена единицы товара (продукции) на территориях а и в.
, где Ра, Рв – цена единицы товара (продукции) на территориях а и в.
В качестве весов здесь можно использовать структуру продажи данных товаров (продукции) по более крупной территории (республике, например).
2) При втором способе расчета учитывается соотношение весов сравниваемых территорий. Рассчитывается средняя цена каждого товара по двум территориям вместе:
(35) 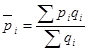 , потом индекс цен
, потом индекс цен 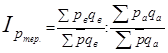 (36)
(36)
Данный подход к расчету территориального индекса цен обеспечивает взаимосвязь: 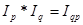
Индекс физического объема товарооборота (производства) имеет вид:
.(37) 
Тогда система индексов имеет вид:
(38) 
Тема 11. Статистическое изучение взаимосвязей явлений.
11.1. Задачи статистики в изучении взаимосвязи явлений.
11.2. Методы корреляционно-регрессионного анализа связи.
11.3. Корреляционно-регрессионный анализ связи парной корреляции.
11.4. Понятие множественной регрессии.
11.1. Задачи статистики в изучении взаимосвязи явлений.
Изучение взаимосвязей экономических явлений особенно важно в условиях рыночной экономики, когда необходимо изучить механизм рыночных связей, соотношение спроса и предложения, издержек производства и дохода (прибыли), спрогнозировать динамику и конъюнктуру рынка, рационально организовать бизнес, управление и многое другое.
При этом важно не только установить факт наличия связи между показателями, но и количественно оценить эту связь, выявить закономерность развития изучаемого явления и влияние на это развитие различного рода факторов. Эти задачи решает статистика. Основная задача её – определить количественные характеристики выявленной на основе положений экономической теории связи.
Статистические показатели изучаемых социально-экономических явлений могут состоять между собой в 3-х основных видах связей: балансовой, компонентной и факторной.
1) Балансовая связь – характеризует зависимость между источниками формирования ресурсов (средств) и их использованием. например, формула товарного баланса:
Он + П = В + Ок , где Он - остаток товара на начало периода,
П – поступление товара за период,
В – выбытие товара за период,
Ок - остаток товара на конец периода.
2) Компонентная связь – когда изменение статистического показатели определяется изменением компонентов, входящих в него как множители.
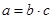
Используется в индексном методе:
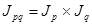 , выявляет роль отдельных факторов на сложный показатель, кроме того, можно найти недостающий показатель.
, выявляет роль отдельных факторов на сложный показатель, кроме того, можно найти недостающий показатель.
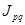 - индекс товарооборота,
- индекс товарооборота, 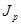 - цен,
- цен,  - объёма товаров.
- объёма товаров.
3) Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей; при этом одни показатели выступают факторные, а другие как результативные. Этот вид связи является причинно-следственной или детерминированной зависимостью.
Факторные связи могут быть:
а) функциональные;
б) корреляционные.
а) При функциональной связи (жёсткая, прямая) изменение результативного признака “y” зависит прямо от действия факторного признака “x”:
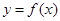 , например, l=2πr (длина окружности).
, например, l=2πr (длина окружности).
б) При корреляционной связи изменение  обусловлено влиянием факторного признака
обусловлено влиянием факторного признака  частично, т.к. влияют и другие факторы:
частично, т.к. влияют и другие факторы:
 , (
, (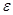 - случайная величина).
- случайная величина).
Корреляционная связь – это соотносительная связь, например, сумма издержек обращения зависит от объёма товарооборота, но и от других факторов: сезонности и других неучтённых факторов.
Характерной особенностью функциональной связи является то, что она проявляется с одинаковой силой у каждой единицы совокупности, следовательно, установив закономерность по отдельность по отдельной единице, её можно распространить на всю совокупность.
При корреляционных связях на одно значение факторного признака возможны различные значения результативного признака, т.к. есть другие факторы, различаемые по направлению и силе воздействия на результат. Следовательно, в данном случае, конкретному изменению факторного признака соответствует среднее изменение результативного признака.
Корреляционные связи изучаются по массовым эмпирическим данным, получаемым при статистическом наблюдении, в которых отображается совокупное действие всех причин и условий на изучаемый показатель.
При статистическом изучении корреляционной связи применяется способ научной абстракции, т.е. определяется влияние только учтённых факторов, а прочие игнорируются. Это упрощает (аппроксимирует) реальный механизм связи, но позволяет установить закономерность взаимодействия исследуемых показателей и получить количественные характеристики связи.
Таким образом, основными задачами статистики связей являются:
1) проверка положений экономической теории о возможности связи между изучаемыми показателями и придание выявленной связи аналитической формы зависимости;
2) установление количественных оценок тесноты связи, характеризующих силу влияния факторных признаков на результативный.
11.2. Методы корреляционно-регрессионного анализа связи.
Первая задача статистики – выявить связь между показателями и придать ей аналитическую форму зависимости.
Основой для этого являются математические функции в виде уравнений:
а)  – прямолинейная зависимость (либо
– прямолинейная зависимость (либо 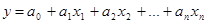 )
)
б) криволинейные зависимости:
ü 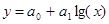 – логарифмическая;
– логарифмическая;
ü 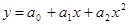 – параболическая;
– параболическая;
ü  – гиперболическая;
– гиперболическая;
ü 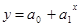 – показательная;
– показательная;
ü  – степенная.
– степенная.
Решить математическое уравнение – определить параметры 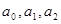 и т.д.:
и т.д.:
1) с помощью метода наименьших квадратов: сумма квадратов отклонений фактических y от выровненных 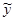 должна быть минимальной. (для линейной зависимости – по формулам в теме “Ряды динамики”);
должна быть минимальной. (для линейной зависимости – по формулам в теме “Ряды динамики”);
2) при численности обследуемой совокупности до 30 единиц необходимо проверить параметры на типичность, т.е. не являются ли параметры уровня регрессии результатом действия случайных величин. Используется t – критерий Стьюдента (специальные таблицы с уровнем значимости α и числом степеней свободы k).
Для этого рассчитываются фактические значения t и сравниваются с табличными:
 и
и  , где n – численность совокупности,
, где n – численность совокупности,
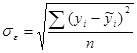 – среднее квадратическое отклонение случайно величины, а
– среднее квадратическое отклонение случайно величины, а 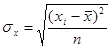 – среднее квадратическое отклонение фактического признака.
– среднее квадратическое отклонение фактического признака.
Параметры уравнения регрессии 
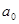 и
и  признаются типичными, если tфакт больше tтабличного:
признаются типичными, если tфакт больше tтабличного: 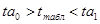

Полученное уравнение регрессии называют математической моделью связи, сущность которой состоит в то, что она определяет среднюю величину результативного признака 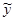 в зависимости от вариации фактического признака
в зависимости от вариации фактического признака 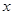 .
.
Вторая задача – определить полученные оценки тесноты связи между 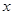 и
и  , она характеризует практическую значимость построенной модели. Для статистической оценки связи применяются показатели вариации:
, она характеризует практическую значимость построенной модели. Для статистической оценки связи применяются показатели вариации:
а) общая дисперсия результативного признака, отображающая влияние всех факторов на 
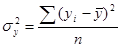

б) факторная дисперсия, отображающая вариацию  только от воздействия
только от воздействия 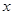
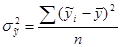
в) остаточная дисперсия – характеризует вариацию y от всех прочих факторов (неучтённых, случайных).
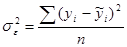
Соотношение между факторной и общей дисперсии характеризует меру тесноты связи между 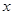 и
и 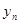 называется коэффициентом детерминации.
называется коэффициентом детерминации.
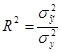 (доля фактической дисперсии в общей, т.е. какая часть общей вариации результативного признака
(доля фактической дисперсии в общей, т.е. какая часть общей вариации результативного признака  объясняется
объясняется 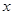 ).
).
Второй показатель тесноты связи называется коэффициентом корреляции:
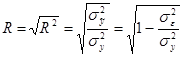 (для ЭВМ).
(для ЭВМ).
При прямолинейной связи рассчитывается линейный коэффициент корреляции:
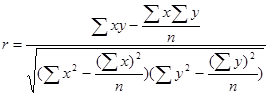 ,
,
R = r только при прямолинейной связи.
Показатели тесноты связи проверяются на существенность – по критерию t (Стъюдента) и F (Фишера).
 ,
, 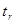 должен быть больше
должен быть больше  – тогда существенен коэффициент
– тогда существенен коэффициент  .
.
Для R – по критерию Фишера:
 ,
,  – число параметров в уравнении;
– число параметров в уравнении; 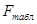 c
c 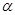 и двумя числами степеней свободы
и двумя числами степеней свободы 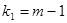 ,
,  .
. 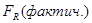 должен быть больше
должен быть больше 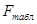 .
.
Для получения выводов о практической значимости показателей тесноты связи даётся оценка по шкале Чеддока:
| R(r) | Сила связи | 
|
| отсутствие связи |
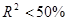
| |
| 0,1-0,3 | слабая | |
| 0,3-0,5 | умеренная | |
| 0,5-0,7 | заметная | |
| 0,7-0,9 | высокая |
 (модель пригодна)
(модель пригодна)
|
| 0,9-0,99 | Весьма высокая (близкая к функциональной, R=1) |
Для выбора адекватного (наиболее соответствующего фактическим данным) уравнения регрессии из множества уравнений применяется показатель средней ошибки аппроксимации:
 ; чем она меньше, тем модель адекватнее.
; чем она меньше, тем модель адекватнее.
11.3. Корреляционно-регрессионный анализ связи парной корреляции.
Парная корреляция (рассматривалась во втором вопросе) – методология, рассматривающая влияние вариации факторного признака x на результат y, т.е. взаимосвязь пары признаков x и y. Применение: на примере – выбрать адекватную модель (на базе данных по однотипным предприятиям зависимости затрат на ремонт оборудования от возраста оборудования.
| № | Возраст оборудования; лет
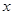
| Затраты на ремонт, тыс. руб.

| 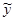 по прямолинейной
по прямолинейной
| 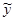 по логарифми-ческой
по логарифми-ческой
| 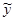 по показа-тельной
по показа-тельной
|
| 1,5 | 0,868 | 0,65 | 1,36 | ||
| 2,0 | 1,479 | 1,54 | 1,64 | ||
| 1,4 | 1,479 | 1,54 | 1,64 | ||
| 2,3 | 2,090 | 2,27 | 1,99 | ||
| 2,7 | 3,312 | 3,42 | 2,93 | ||
| 4,0 | 4,534 | 4,31 | 4,31 | ||
| 2,3 | 3,312 | 3,42 | 2,93 | ||
| 2,5 | 2,700 | 2,89 | 2,41 | ||
| 6,6 | 5,145 | 4,70 | 5,23 | ||
| 1,7 | 2,090 | 2,27 | 1,99 | ||
| Итого: | 27,0 | 27,009 | 27,01 | 26,43 |
Определяется путём перебора наиболее часто применяемых уровней регрессии:
а) прямолинейной функции: 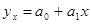 ;
;
б) логарифмической функции:  ;
;
в) показательной функции: 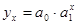 .
.
Сравниваться должны два критерия: остаточная дисперсия – должна быть минимальна для определения адекватных моделей и средняя ошибка аппроксимации – должна быть минимальна.
Параметры находятся по методу наименьших квадратов, для показательной – через логарифм.
а)  , б)
, б)  , в)
, в)  .
.
Параметры проверяются на типичность, для чего рассчитывается 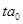 и
и  -фактические, число степеней свободы
-фактические, число степеней свободы  и через
и через 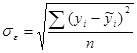 и
и 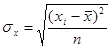 .
.
а)  б)
б)  в)
в) 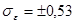
остаточная дисперсия а) 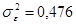 б)
б) 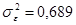 в)
в) 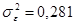 .
.
Параметры везде получаются значимы.
Практическая значимость моделей оценивается по R(r): 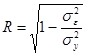 и
и 
а) 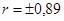 б)
б) 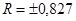 в)
в) 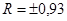
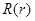 проверяется по F-крит. с
проверяется по F-крит. с 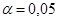 ,
, 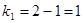
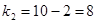 – везде значимы.
– везде значимы.
а) 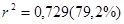 – может быть использована для практических целей;
– может быть использована для практических целей;
б) 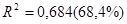 – может быть пригодна;
– может быть пригодна;
в) 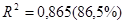 – может быть пригодна.
– может быть пригодна.
Далее модели проверяются на адекватность через показатель средней ошибки аппроксимации.

а) 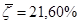 б)
б) 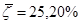 в)
в) 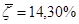 .
.
Следовательно, наиболее адекватной является экономико-математическая модель, построенная по показательной функции.
11.4. Понятие множественной регрессии.
На практике чаще всего возникает необходимость исследовать зависимость результативного признака от нескольких факторных признаков. Тогда статистическая модель представляется уравнением регрессии с несколькими переменными величинами. Такая регрессия называется множественной.
Множественная линейная регрессия имеет вид:
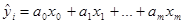 , где
, где  – фиктивная переменная.
– фиктивная переменная.
Параметры уравнения определяются МНК, при этом значения x и y представляются в матричном виде:
 матрица
матрица 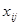 - значений независимых переменных.
- значений независимых переменных.
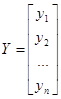 вектор значений зависимый переменной
вектор значений зависимый переменной 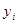 .
.
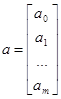
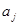 - вектор оценок параметров.
- вектор оценок параметров.
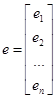 вектор ошибок
вектор ошибок 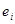 .
.
Тогда: линейная модель в векторном виде
 .
.
Вектор оценки 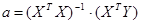 , где
, где  - транспонированная матрица, строки исходной матрицы в транспонированной становятся столбцами,
- транспонированная матрица, строки исходной матрицы в транспонированной становятся столбцами, 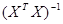 - обратная матрица.
- обратная матрица.
 , где
, где 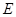 - единичная матрица.
- единичная матрица.
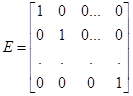 .
.
Например, сравнить параметры (коэффициенты регрессии) в уравнении нельзя, если они не выражаются в одинаковых единицах.
Для сравнения применяют нормированные коэффициенты регрессии 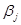 (бетта-коэффициент): он показывает величину изменения результативного признака при изменении факторного признака
(бетта-коэффициент): он показывает величину изменения результативного признака при изменении факторного признака 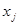 на одну среднюю квадратическую ошибку (в единицах измерения ошибки):
на одну среднюю квадратическую ошибку (в единицах измерения ошибки):
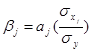 , где
, где 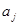 - параметр при
- параметр при 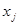 факторе,
факторе, 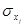 - средне квадратическое отклонение факторного признака,
- средне квадратическое отклонение факторного признака, 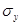 - среднее квадратическое отклонение результативного признака.
- среднее квадратическое отклонение результативного признака.
Анализ дополняется расчётом коэффициента эластичности факторных признаков
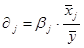 - он показывает, на сколько процентов измени
- он показывает, на сколько процентов измени
Date: 2016-01-20; view: 1643; Нарушение авторских прав