Характеристика закономерности рядов распределения. Кривые нормального распределения

С помощью рядов распределения статистика решает одну из своих задач: характеризует и измеряет колеблемость варьирующего признака. В вариационных рядах существует связь между частотами и значениями варьирующего признака: с увеличением признака величина частоты сначала возрастает до определённой границы, а потом уменьшается. Такие изменения называются закономерностями распределения.

Статистические данные рядов распределения по конкретному признаку в графическом виде представляют собой определенные кривые распределения. Задачей статистики является определить форму кривой (тип), степень рассеивания (чем больше рассеяна кривая, тем больше колеблемость признака), степень её асимметрии, высоко- или низковершинность. Цель такого исследования – проверить нормальность условий отбора данных, т.е. если кривая асимметрична или имеет две и более вершины, то состав данных разнотипен, их необходимо перегруппировать и выделить другие, более однородные группы.

Для определения характера распределения оценивают степень его однородности, т.е. вычисляют показатели асимметрии и эксцесса.

Симметричным (нормальным) распределением является то, у которого частоты двух вариант, равностоящих в обе стороны от центра распределения, равны между собой. В нём , Mo и Me равны, т.е. показатели асимметрии равны нулю. В противном случае рассчитываются показатели асимметрии:

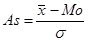(7.27) или 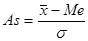(7.28).

Они могут быть положительными и отрицательными. Если показатель асимметрии положительный (As>0), значит, присутствует правосторонняя асимметрия и .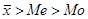

Если показатель асимметрии отрицательный (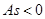), то асимметрия левосторонняя и .

Коэффициент асимметрии может изменяться от (-3) до (+3). Принято считать, что асимметрия больше 0,5 (независимо от знака) – значительная, меньше 0,25 – незначительная.

На практике чаще применяется показатель асимметрии:

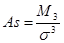(7.29), где 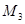- центральный момент третьего порядка*, 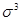- среднее квадратическое отклонение в кубе.

В действительности распределения данных редко бывают симметричными, т.е. нормальными. Нормальная кривая – это идеализированная форма распределения, хотя многие распределения близки к нормальному.

Преобразование фактического конкретного распределения в нормальное, т.е. определение теоретической кривой нормального распределения, необходимо, чтобы выявить общую закономерность развития изучаемого явления, возникающую под воздействием множества случайных причин, позитивных и негативных отклонений. Уравнение нормальной кривой:

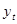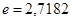
(7.30), где - ордината, , 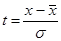- стандартизированная нормальная величина.

Широко применяется в теории выборочного метода для определения закономерности развития генеральной совокупности по данным выборки и для расчёта соответствующих показателей.

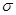Из формулы (7.30) видно, что и определяют черты симметричной кривой нормального распределения. В зависимости от их значений, кривая может иметь разный центр группирования, быть более удлинённой или сжатой.

Для симметричных распределений рассчитываются показатели эксцесса (островершинности):

1) показатель Линдберга:

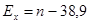(7.31), где n – доля (%) количества вариант, лежащих в интервале, равном половине 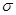в ту или другую сторону от .

2) (7.32), где 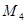- центральный момент 4-го порядка, 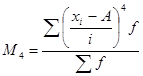(7.33), где

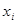- середина интервала в интервально ряду, 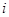- величина интервала.

Если 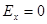, то распределение симметричное;

Если , то распределение островершинное;

Если 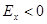, то распределение плосковершинное.

Оценка существенности показателей асимметрии и эксцесса необходима для вывода об отнесении данного эмпирического распределения к типу нормального распределения. Если оно не относится к нормальному, то строится математическая модель по уравнению (7.30) и выявляется закономерность развития данного явления, включая и прогноз.

Существенность расхождений между эмпирическим и теоретическим распределениями определяется с помощью ряда критериев согласия: К. Пирсона (Хи-квадрат), В.И.Романовского, Б. С. Ястремского, А. Н. Колмогорова.

Контрольные вопросы.

1. Что такое вариация признака?

2. Перечислите абсолютные и средние показатели вариации.

3. Как исчисляется размах вариации?

4. Что представляет собой среднее линейное отклонение?

5. Какой показатель вариации называется дисперсией? По каким формулам она рассчитывается?

6. Каковы основные свойства дисперсии?

7. Что называется средним квадратическим отклонением? По какой формуле оно вычисляется?

8. Назовите относительные показатели вариации.

9. Определите значение коэффициента вариации для экономического анализа.

10. Как исчисляется дисперсия альтернативного признака?

11. Как определяются межгрупповая и средняя из внутригрупповых дисперсии?

12. В чем состоит практическое значение правила сложения дисперсий?

13. Какое распределение называется нормальным?

Заключение

Важнейшей задачей дисциплины «Статистика» является подготовка специалистов в системе экономического образования, владеющих различными методами сбора, систематизации и анализа сведений, характеризующих развитие экономической, социальной и других сфер общественной жизни. Статистика для студентов, обучающихся по экономическим специальностям, служит основой для изучения, совершенствования методов экономического анализа и, главное, для приобретения практических навыков проведения такого анализа и расчета различных экономических показателей.

В рамках учебного пособия невозможно дать исчерпывающие ответы на все вопросы, возникающие в ходе изучения дисциплины. Данное учебное пособие «Общая теория статистики» дает общее представление о статистике как науке, об организации государственной статистики в нашей стране и о ее значении в развитии рыночной экономики. Основная задача пособия – дать правильное представление студентам о предмете статистики, о статистической методологии, о практической значимости применения методов расчета различных показателей, необходимых при изучении и анализе текущего положения в экономической и социальной сферах, а также о методах прогнозирования тенденций развития общественной жизни.

Изучаемая студентами экономических специальностей дисциплина «Общая теория статистики» дает им основу для дальнейшего теоретического обучения по другим экономическим дисциплинам и навыки применения статистических методов в экономическом анализе.

Date: 2016-01-20; view: 657; Нарушение авторских прав