Абсолютные и средние показатели вариации. Показатели относительного рассеивания. Дисперсия альтернативного признака

I. К абсолютным и средним показателям вариации относятся:

1) Размах вариации: . (7.1) Самый простой показатель по расчёту, но улавливает только крайние отклонения, не отражает отклонений всех вариант в ряду. Измеряется в тех же единицах, что и варианты.

2) Среднее линейное отклонение:

(7.2) или (7.3)

Это средняя арифметическая из отклонения индивидуальных значений признака от средней величины, без учёта знака этих отклонений, т.к., по правилу средней арифметической, сумма фактических отклонений от средней равна нулю.

Показатель даёт обобщающую характеристику распределению отклонений, учитывает различия всех единиц совокупности. Чем оно меньше в данной совокупности, тем однороднее её показатели, по сравнению с показателями другой сравниваемой совокупности.

В статистической практике применяется редко, т.к. часто не улавливает степень рассеивания. Единица измерения та же, что у вариант.

3) Дисперсия (мера вариации) или средний квадрат отклонений:

(7.4) или (7.5)

Это средняя арифметическая из возведенных в квадрат отклонений вариант от средней величины. Не имеет единиц измерения.

4) Среднее квадратическое отклонение: это квадратный корень из дисперсии (7.6). Оно характеризует вариацию признака в абсолютном выражении, измеряется в тех же единицах, что и признак (варианта).

Дисперсия и среднее квадратическое отклонение являются общепринятыми мерами вариации признака.

Среднее квадратическое отклонение является критерием надёжности средней величины. Чем оно меньше, тем лучше средняя арифметическая отражает изучаемую совокупность.

Кроме того, если средняя величина отражает тенденцию развития, т.е. влияние главных факторов на изменение признака, то среднее квадратическое отклонение измеряет силу воздействия прочих факторов.

Математические свойства дисперсии:

1) Если из всех значений вариант отнять постоянное число A, то дисперсия от этого не изменится.

2) Если все значения вариант разделить на постоянное число A, то дисперсия уменьшится в A² раз, а среднее квадратическое отклонение – в A раз.

3) Дисперсия от постоянной величины A, которая отличается от средней арифметической, т.е. не равна ей, будет всегда больше дисперсии, исчисленной от средней арифметической () на определённую величину, равную , т.е.

(7.7) или

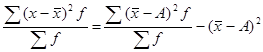(7.8).

Дисперсия от средней всегда меньше, чем дисперсии, рассчитанные от любых других величин. Если A=0, то тогда (1) преобразуется в

(7.9) или 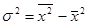(7.10).

Формула (7.10) – это второй способ расчёта дисперсии как разности между средним квадратом значений признака и квадратом среднего значения признака.

Если в этой формуле условно обозначить , а и применить второе свойство дисперсии, разделив все варианты на величину интервала, то

(7.11), где (7.12) - момент первого порядка, (7.13) - момент второго порядка.

Этот способ расчёта дисперсии называется способом моментов (способ отсчёта от условного нуля). Применяется только при условии равных интервалов в вариационном ряду.

II. Показатели относительного рассеивания.

Характеризуют колеблемость (вариацию) признака в относительных величинах, т.е. относительную меру колеблемости. Рассчитываются, когда сравнивается один признак в двух одноимённых совокупностях, но относящихся к разным единицам наблюдения, при различных значениях средних в этих совокупностях, а также при сравнении разнородных совокупностей. К относительным показателям относятся:

1) Коэффициент осцилляции: (7.14), отражает относительную колеблемость крайних значений признака вокруг средней.

2) Относительной линейное отклонение: (7.15), характеризует долю усреднённого значения абсолютных отклонений в средней величине.

3) Коэффициент вариации: 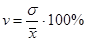(7.16), используется для оценки типичности средних величин. Является критерием надёжности средней: если коэффициент вариации больше 35-40%, то признак сильно колеблется, следовательно, средняя менее надёжна, а совокупность неоднородна.

Часто применяется в тех случаях, когда нельзя сравнить средние квадратические отклонения разных явлений. Например, что больше варьирует: рост мальчиков одного возраста или их вес (в м., см. – рост, вес – в кг., г.). Если , - вес варьирует больше, чем рост.

III. Дисперсия альтернативного признака.

Показатели вариации рассчитываются не только для количественных признаков, но и для альтернативных. Альтернативным называется признак, которым обладают одни единицы совокупности и не обладают другие (два взаимоисключающих варианта: пол – мужской, значит, не женский.)

В статистике наличие альтернативного признака обозначается 1, а его отсутствие – 0. Доля вариантов, обладающих признаком, обозначается «p», а доля вариантов, не обладающих – «q».

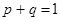(7,17), (7,18), (7,19), (7,20).

Например, из 1000 человек, работающих на предприятии, 600 человек составляют женщины, 400 человек – мужчины.

, , , .

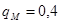Date: 2016-01-20; view: 997; Нарушение авторских прав