Пример расчета средней арифметической в дискретном ряду

Следовательно, среднее число детей в семье определяется делением: (170:100). Оно получается равным 1,7 ребенка.

Методика расчета средней арифметической в интервальном ряду приведена в таблице 2.

Таблица 10

Расчет средней арифметической в интервальном ряду

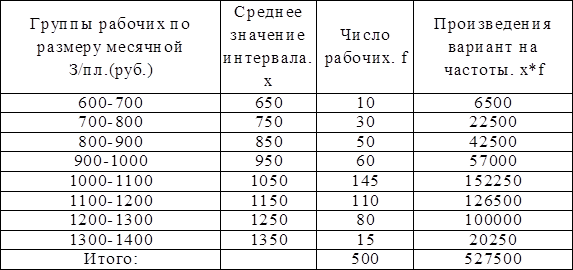
Для расчета средней в интервальном ряду надо перейти к дискретному ряду, т.е. по каждой группе исчисляется средняя по простой арифметической.

При наличии открытых интервалов (например, до 700руб. или 1300 рублей и более), их необходимо преобразовать в закрытые. Для этого берут значение величины интервала как у последующего интервала или предыдущего.

Свойства средней арифметической

1) произведение средней на сумму частот равно сумме произведений вариант на частоты.
(6.4)

2) если от каждой варианты отнять какое-либо число, то новая средняя уменьшится на то же число
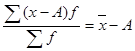(6.5)

3) если к каждой варианте прибавить какое-либо число, то новая средняя увеличится на то же число
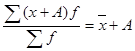(6.6)

4) если каждую варианту разделить на какое-либо число, то средняя арифметическая уменьшится во столько же раз
(6.7)

5) если каждую варианту умножить на какое-либо число, то средняя арифметическая увеличится во столько же раз
(6.8)

6) если все частоты разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится так как не изменится удельный вес каждой частоты:
2, 6, 10, 12, 29, 22, 16, 3 в сумме дадут 100.

7) сумма отклонений вариант от средней арифметической всегда равняется 0

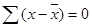(6.9)

Эти свойства применяются для упрощения расчетов средней, особенно в интервальных рядах

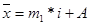, где (6.10), где

m₁ – момент первого порядка

i – величина интервала

A – произвольная постоянная величина, обычно центральная варианта ряда.

Такой способ расчета средней называется способом моментов или способом отсчета от условного нуля.

II. Средняя гармоническая – это величина, обратная средней арифметической, то есть рассчитанная из обратных значений признака. Применяется, когда веса (частоты) приходится не умножать, а делить на варианты или умножать на их обратные значения.

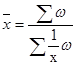(6.11), где w=x*f

Таблица 11

Расчет среднего процента выполнения плана.

1) 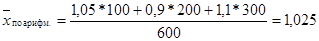(102,5%)

2) - если за веса взять факт, то есть нет данных по плану
(102,5%),

то есть средняя гармоническая применяется, когда нет данных о частотах (весах) по отдельным вариантам, но есть информация об их произведении. На практике чаще применяется средняя гармоническая взвешенная (как в примере). Существует также средняя гармоническая простая. Она применяется, если произведения (объемы явлений) по каждому признаку равны.

III. Средняя геометрическая – средний показатель, который вычисляется как корень n-ой степени из произведения вариант х (х1,х2…)
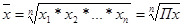(6.12)

IV. Средняя квадратическая – показатель вариации признака,
(6.13)

Date: 2016-01-20; view: 877; Нарушение авторских прав