Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Показатели вариации
|
|
К абсолютным показателям вариации относятся:
Размах вариации (R) – определяется по формуле
R =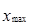 
– 
.
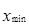Среднее квартильное отклонение (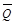
) – рассчитывают по формуле
.
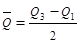Среднее линейное отклонение (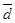
) – рассчитывают по формулам
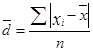– для не сгруппированных данных;
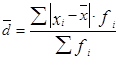– для сгруппированных данных.
Дисперсия (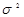
) – вычисляется по формулам
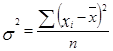– для не сгруппированных данных;
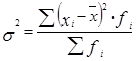– для сгруппированных данных.
Среднее квадратическое отклонени е (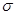
) – вычисляется по формулам
– для не сгруппированных данных;
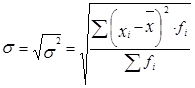– для сгруппированных данных.
Показатель среднего квадратического отклонения используется при оценке меры риска при принятии финансово-экономических решений. Чем меньше величина σ, тем меньше возможный риск.
К относительным показателям вариации относятся:
– коэффициент квартильной вариации ( 
)
= 
.
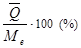– коэффициент осцилляции(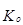 
)
= 
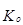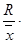100 (%).
– коэффициент вариации (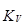 
)
.
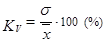Исходная совокупность считается однородной по изучаемому признаку, если коэффициент вариации не превышает 33%. Коэффициент вариации применяется при сравнении степени вариации в различных совокупностях.
Пример 10. По приведенным условным данным о размере и числе соответствующих штрафов вычислить показатели вариации.
| Размер штрафа, руб. | Число штрафов, единиц |
| 80–100 | |
| 100–120 | |
| 120–140 | |
| 140–160 | |
| 160–180 | |
| Итого |
Решение. Исходные данные являются сгруппированными, поэтому для расчета необходимых показателей будем применять взвешенные формулы. Все предварительные расчеты представим в следующей таблице:
|
|
| 
|
|
|
|
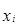
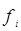
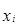
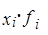
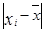
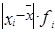
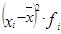
| 80–100 | 4 050 | |||||
| 100–120 | 3 750 | |||||
| 120–140 | ||||||
| 140–160 | 1 200 | 1 800 | ||||
| 160–180 | 4 900 | |||||
| Итого | 3 240 | 14 600 |
1. Размах вариации R =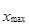 
– 
= 180 – 80 = 100 руб.
2. Средний размер штрафа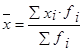 
руб.
3. Среднее линейное отклонение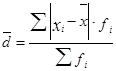 
= = 
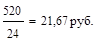
4. Дисперсия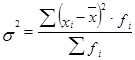 
= 
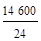= 608,3.
5. Среднее квадратическое отклонение 
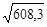= = 24,66 руб. Это значит, что в среднем размер каждого штрафа отличается от среднего размера штрафа (
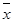= 135 руб.) на 24, 66 руб.
6. Коэффициент вариации: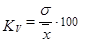 
= 
= 18,3 %.
Поскольку величина данного коэффициента меньше 33%, то можно сделать вывод об однородности исходной совокупности штрафов по их размеру.
Основные математические свойства дисперсии:
– дисперсия, рассчитанная по отношению к средней величине, является минимальной;
– дисперсия постоянной величины равна нулю;
– если все индивидуальные значения признака (варианты) увеличить (уменьшить) на какое-то постоянное число А, то дисперсия новой совокупности не изменится;
– если все индивидуальные значения признака (варианты) увеличить (уменьшить) в k раз (где k – постоянное число, отличное от нуля), то дисперсия новой совокупности увеличится (уменьшится) в k 2 раз;
– если вычислена дисперсия по отношению к числу В, отличному от средней величины, то дисперсию исходной совокупности можно рассчитать по соотношению:
;
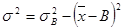– дисперсию исходной совокупности можно рассчитать как разность между средней квадратов признаков и квадратом средней величины:
.
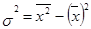Date: 2016-01-20; view: 581; Нарушение авторских прав