Функция включения

Функцией включения (функцией Хевисайда) называется функция

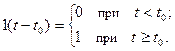
(9.62)

При t₀ = 0 для функции включения обозначение 1(t) (рис. 6.14). График функции 1(t - t₀) имеет вид ступеньки или скачка, высота которого равна 1.

9.12. К определению функции включения

Функцию Хевисайда 1(t - t₀) удобно использовать для аналитического представления внешних воздействий на цепь, значение которых скачкообразно изменяется в момент коммутации:

(9.63)

где f(t) - ограниченная функция времени.

1) При подключении цепи к источнику постоянного тока или напряжения значение внешнего воздействия на цепь

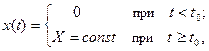
(9.64)

где t₀ - момент коммутации.

Используя функцию Хевисайда, выражение (9.64) можно представить в виде

x(t) = X 1(t - t₀).

а б в

Рис. 9.13. Представление прямоугольного импульса в виде разности 2 неединичных скачков

2) В цепь включается источник гармонического тока или напряжения при t = t₀

С использованием функции 1(t - t₀) внешнее воздействие на цепь можно представить в форме

x(t) = 1(t - t₀)>X_m cos(wt + ψ).

3) Внешнее воздействие на цепь в момент времени t = t₀ скачкообразно изменяется от одного фиксированного значения Х₁ до другого Х₂,

X(t) = X₁ + (X₂ - X₁) 1(t - t₀).

4) Внешнее воздействие на цепь, имеет форму прямоугольного импульса высотой Х и длительностью t_и (рис. 6.15? a). Его можно представить в виде разности двух одинаковых скачков

X₁(t) = X 1(t - t₀)

и X₂(t) = Х 1(t - t₀ - δ),

сдвинутых во времени на δ (рис. 6.15, б, в):

Х(t) = Х₁(t) - Х₂(t) = X(1(t - t₀) - 1(t - t₀ - δ)). (9.65)

δ-функция

δ-функция или функция Дирака определяется как

δ-функция может быть представлена как импульс бесконечно малой длительности, бесконечно большой высоты, площадь которого равна 1 (рис. 9.14, а)

а б в

Рис. 9.14. К определению d- функции

Следовательно,

(9.66)

При t₀ = 0 для d-функции используется обозначение d(t). При построении временных диаграмм функции d(t - t₀) и d(t) будем изображать в виде вертикальной стрелки (рис. 9.14, б, в).

Для установления связи между d- функцией и функцией включения воспользуемся выражением (9.65). Полагая X = 1/Dt и устремляя Dt к нулю, получаем

(9.67)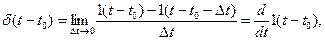

откуда

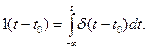
(9.68)

Таким образом, d-функция представляет собой производную от функции включения, а функция включения - интеграл от d-функции.

Строгое обоснование операции над единичными функциями, в том числе операции дифференцирования, дано в теории обобщенных функций. Для качественного обоснования таких операций функции 1(t - t₀) и d(t - t₀) удобно рассматривать в качестве предельных значений некоторых более простых функций, для которых соответствующие операции являются определенными.

При выполнении различных операций над единичными функциями момент коммутации t₀ удобно расчленять на три различных момента: t_0- - момент времени, непосредственно предшествовавший коммутации, t₀ - собственно момент коммутации и t₀₊ - момент времени, следующий непосредственно после коммутации. С учетом этого интеграл (9.66) можно заменить на

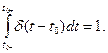
(9.69)

В общем случае

(9.70)

Произведение произвольной ограниченной функции времени f(t) на d(t - t₀)

следовательно,

f(t) d(t - t₀) = f(t₀) d(t - t₀). (9.71)

Из выражений (9.70) и (9.71) следует, что интеграл от произведения произвольной ограниченной функции f(t) на d (t - t₀) равен либо значению этой функции при t = t₀ (если точка t₀ принадлежит интервалу интегрирования), либо 0 (если точка t₀ не принадлежит интервалу интегрирования

(9.72)

Таким образом, с помощью d-функции можно выделять значения функции f(t) в произвольные моменты времени t₀. Эту особенность d-функции обычно называют фильтрующим свойством.

Для определения реакции линейных электрических цепей на внешнее воздействие в виде единичного скачка или единичного импульса необходимо найти изображения единичных функций по Лапласу. Используя рассмотренные свойства единичных функций, получаем

(9.73)

При t₀ = 0 операторные изображения единичных функций имеют простой вид:

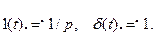(9.74)