Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Свойства преобразования Лапласа
|
|
1) Изображение по Лапласу постоянной величины К равно этой величине, деленной на р:
(9.33)
2) Умножение функции времени a(t) на постоянное число К соответствует умножению на это же число ее изображения:
(9.34)
3) Изображение суммы функций времени равно сумме изображений этих функций:
(9.35)
где 
4) Теорема дифференцирования. Если начальное значение функции a(t) равно нулю (а(0+) = 0), то дифференцированию функции a(t) соответствует умножение изображения этой функции на р
(9.36)
при а(0+) ¹ 0
(9.37)
5) Теорема интегрирования. Интегрированию функции времени в пределах от 0 до t соответствует деление изображения этой функции на р
|
6) Теорема запаздывания. Смещению функции времени на t0 соответствует умножение изображения на 
(9.39)
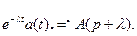7) Теорема смещения Смещению изображения А(р) в комплексной плоскости на комплексное число l соответствует умножение оригинала на 
.
8) Теорема разложения. Если изображение А(р) может быть представлено в виде отношения двух полиномов от р, не имеющих общих корней
(9.40)
причем степень полинома М(p) выше, чем степень полинома N(p), а уравнение
M(p) =0 (9.41)
не имеет кратных корней, то для перехода от изображения к оригиналу можно воспользоваться формулой:
(9.42)
где pk - корни уравнения (9.41).
При использовании операторного метода решения дифференциальных уравнений неизвестные токи и напряжения ветвей электрической цепи, а также заданные токи и напряжения независимых источников заменяют их операторными изображениями. При этом система интегро-дифференциальных уравнений электрического равновесия, составленная относительно мгновенных значений токов и напряжений ветвей, преобразуется в систему алгебраических уравнений, составленных относительно операторных изображений соответствующих токов и напряжений. Решая эту систему уравнений, находят изображения искомых токов и напряжений ветвей электрической цепи после коммутации. Далее, применяя обратное преобразование Лапласа, переходят от изображений искомых токов и напряжений к оригиналам.
Date: 2016-02-19; view: 521; Нарушение авторских прав