Способы описания динамических характеристик

1. дифференциальные уравнения или системы дифференциальных уравнений в полных или частных производных. В простейшем случае это одно дифференциальное уравнение, связывающее входные и выходные величины.

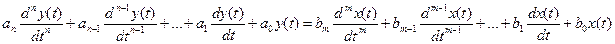
у – выходная величина

x – входная величина

t –время (реальная координата)

Для линейных систем коэффициенты постоянны (a, b = const). Это для стационарных систем. Мы будем рассматривать только стационарные системы.

Если входные и выходные величины по всему объему объекта являются одинаковыми, то такие объекты называются с сосредоточенными параметрами, соответственно такие системы описываются дифференциальными уравнениями в полных производных. Если эти величины не одинаковы по всему объему, добавляются еще пространственные координаты, и система описывается дифференциальными уравнениями в частных производных.

В правую часть уравнения могут входить еще и возмущения. Структура этой составляющей та же, что и входная величина x.

Дифференциальные уравнения обычно дополняются начальными и граничными условиями.

Начальные условия:

Граничные условия:

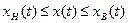
в – верхнее значение

н – нижнее значение

Хотя дифференциальные уравнения и являются универсальным способом описания динамики, на практике ими пользоваться неудобно, так как простые решения имеют только дифференциальные уравнения первого и второго порядка.

1. частотные характеристики.

Они предполагают воздействие на систему (входной величины) в виде гармонических колебаний и регистрации при этом выходной величины.

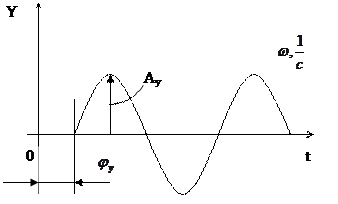
Итак, если на вход линейной системы подать гармонический (синусоидальный) сигнал с частотой , фазой и амплитудой А_x, то через некоторое время, связанное с установлением режима, выходная величина так же начнет меняться с той же частотой , но с амплитудой А_y и фазой .

Можно проводить такой опыт и при других частотах .

Тогда:

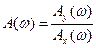- амплитудно-частотная характеристика

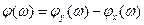- фазочастотная характеристика

Для простых объектов АЧХ имеет следующий вид:

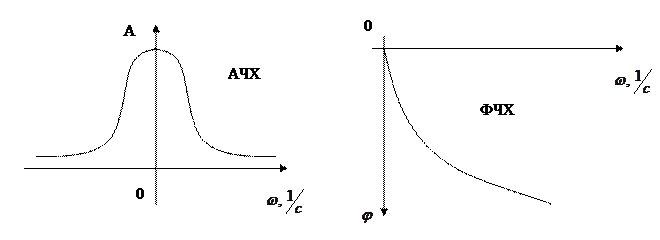
Существует комплексная характеристика АФЧХ (строится на комплексной плоскости).

Единица на вещественной оси соответствует = 0, а начало координат соответствует = ∞.

Геометрическое место точек, описывающих конец вектора при других частотах называется годографом. Длина вектора равна амплитуде, а угол фазе частотной характеристики.

Частотные характеристики широко используются в электротехнике. В машиностроении, а также химической технологии используются реже.

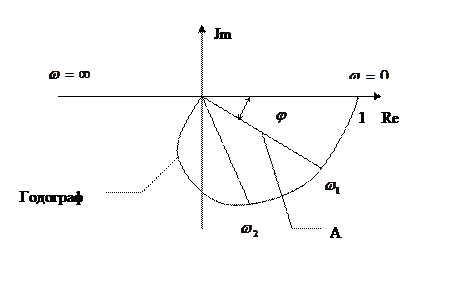
Re – вещественная ось

Jm – мнимая ось

1. временные характеристики. Они представляют собой реакцию выходной величины на стандартное воздействие, т.е. изменение входной величины по определенному закону. В качестве стандартного воздействия используется:

Единичный скачок. Единичный импульс.

h(t) – переходная характеристика (переходная функция).

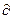(t) – импульсная функция (весовая функция). Площадь импульса равна единице (единичный импульс).

Временные характеристики, а именно переходная, широко используется и в химической технологии, и в машиностроении, и в других отраслях.

В теории автоматического управления для упрощения решения (определения выходной величины при различных законах ее изменения) используется операционное исчисление. В основе операционного исчисления лежит преобразование Лапласа.

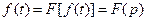
- оригинал

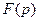- изображение (по Лапласу)

В теории управления используется одностороннее преобразование, т.к. время изменяется от 0 до ∞, поэтому вместо -∞ ставится 0 в отличии от классической математики.

Обратное преобразование:

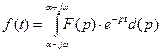
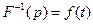
р – мнимый аргумент.