Метод интегрирования заменой переменной в интеграле

Для вычисления интеграла вида 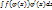используя равенство записывают его в форме. Далее заменяя φ(x) на u и вычислив полученный инеграл, проводят обратную замену u на φ(x). , где u=φ(x) это правило замены переменной в неопред. интеграле.

Пусть предел интегральной суммы при стремлении к нулю существует, конечен и не зависит от выбора точек. Тогда этот предел называется определенным интегралом.

Свойства: постоянный множитель можно выносить за знак интеграла; интеграл суммы равен сумме интегралов

Геометрический смысл: площадь

29.Определенный интеграл: определение, основные свойства, геометрический смысл.

Определенным интегралом от ф-ии f(x) на отрезке [a;b] называется предел интегральных сумм S_n при условии, что длина наибольшего частичного отрезка ∆x_i стремится к 0.

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

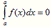
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

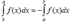
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

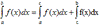
V. Постоянный множитель можно выносить за знак определенного интеграла.

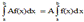
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

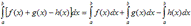
Date: 2016-02-19; view: 444; Нарушение авторских прав