Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Первая теорема Вейерштрасса. Формулировка, доказательство, анализ, применение
|
|
Формулировка:
Если функция определенна и непрерывна в [a;b], то она ограничена. (На этом промежутке)
Доказательство:
1) Ограниченность сверху.
Предположим обратное: пусть f(x) – неограниченна в [a;b] сверху. Тогда " n > N $ 
є [a;b]: f ( ) > n. В таком случае, имеем бесконечную последовательность 
которая ограничена сверху и снизу, так как 
є [a;b]. По лемме Больцано - Вейерштрасса, из неё можно выделить подпоследовательность 
, имеющую конечный предел с є [a;b]. Так как функция непрерывна, а также 
, то 
при чём, 
– конечное число, но так как последовательность 
бесконечная, то 
Таким образом, получаем, что:
|
Но, так как функция непрерывна, то данное выражение образует противоречие, и из этого следует, что изначальное предположение – неверное, и функция ограниченна сверху.
2) Ограниченность снизу.
Предположим обратное: пусть f(x) – неограниченна в [a;b] снизу. Тогда " n > N $ є [a;b]: f ( ) < n. В таком случае, имеем бесконечную последовательность которая ограничена сверху и снизу, так как є [a;b]. По лемме Больцано - Вейерштрасса, из неё можно выделить подпоследовательность , имеющую конечный предел с є [a;b]. Так как функция непрерывна, а также так как , то при чём, – конечное число, но так как последовательность бесконечная, то
Таким образом, получаем, что:
|
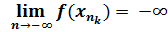
Но, так как функция непрерывна, то данное выражение образует противоречие, и из этого следует, что изначальное предположение – неверное, и функция ограниченна снизу.
Анализ:
Методы, используемые для доказательства теоремы:
· Метод «От противного»;
· Сведение решения задачи к решению подзадач;
· Введение вспомогательного элемента;
Единственное условие теоремы является обязательным. Доказательство: При исключении данного условия, выражения (1) и (2) не будут вызывать противоречие, так как, в таком случае, f(c) может и не быть конечным значением.
Для того, чтобы доказать это достаточно привести хотя бы один пример функции, для которой не выполняется условие, и, для которой заключение теоремы является неверным. Рассмотрим функцию 
, на отрезке [-1;0].
Для данной функции на данном отрезке условие теоремы не выполняется, так как имеется разрыв в точке 0, кроме того неверным является и заключение теоремы, так как y стремится к 
.
Применение:
· Чаще всего используется для доказательства других теорем. (Теорема Ролля, вторая теорема Вейерштрасса и т.д.)
Date: 2016-02-19; view: 1122; Нарушение авторских прав