
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема Дарбу. Формулировка, доказательство, анализ, применение
|
|
Формулировка:
Если функция f(x) определена и непрерывна в [a;b], и если существует конечная производная "x є [a;b], и если f’(a) = A и f’(b) = B, причём A ¹ B, то значение f’(x) сплошь заполняет промежуток между А и В, то есть "С є (A;B) $ c є (a;b): f’(c) = C.
Доказательство:
1) Рассмотрим частный случай: A < 0 и B > 0. Докажем, что $ c є (a;b): f’(c) = C = 0.
По 2-й теореме Вейерштрасса: функция f(x) в некоторой точке c є (a;b) принимает наибольшее (наименьшее) значение. Тогда, по теореме Ферма f’(c) = 0, что и требовалось доказать.
2) Рассмотрим общий случай: A ¹ B. Для определённости, пусть A < B. Нужно доказать, что
"С є (A;B) $ c є (a;b): f’(c) = C. Введём вспомогательную функцию j(x) так, чтобы она удовлетворяла частному случаю:
I. j’(a) < 0.
II. j’(b) > 0.
III. j’(c) = 0 => f’(c) = C.
f’(c) – C = 0 = j’(c) 


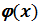 – удовлетворяет условия частного случая $ c є (a;b):
– удовлетворяет условия частного случая $ c є (a;b): 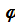 ‘(c) = 0
‘(c) = 0  так как С є (A;B) выбрано произвольно, то это и доказывает, что функция f’(x) сплошь заполняет (A;B).
так как С є (A;B) выбрано произвольно, то это и доказывает, что функция f’(x) сплошь заполняет (A;B).
Анализ:
Методы, используемые для доказательства теоремы:
· Введение вспомогательного элемента;
· Приведение к частному случаю;
· Приведение задачи к уже решенной задаче;
· Дедукция;
· Сведение решения задачи к решению подзадач.
Все условия теоремы обязательны, потому как если исключить хотя бы одно из них, то теорема будет неверна. Также стоит отметить, что из условия существования производной следует, что из второго условия теоремы следует первое. Другими словами, при невыполнении 1-го условия, соответственно не выполняется и 2-е. Обратное, однако, неверно, так как при невыполнении 2-го условия, 1-е может выполняться. Докажем обязательность условий:
Рассмотрим функцию, которая задается неравенством на промежутке [-2;2]:  при
при  и
и  при
при  .Теперь возьмём производную данной функции. Получим, что
.Теперь возьмём производную данной функции. Получим, что  при
при 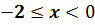 и
и  при
при  . В результате, для данной функции не выполняется первое условие, так как она неопределенна в точке 0. Следовательно, не выполняется и второе условие, по причинам описанным выше. Однако 3-е условие выполняется, так как
. В результате, для данной функции не выполняется первое условие, так как она неопределенна в точке 0. Следовательно, не выполняется и второе условие, по причинам описанным выше. Однако 3-е условие выполняется, так как 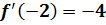 и
и  Тем не менее, заключение теоремы неверно, так как нет таких значений c є (a;b), при которых бы производная достигала значений из промежутка (0;6), а он является вложенным в промежуток (-4;6).
Тем не менее, заключение теоремы неверно, так как нет таких значений c є (a;b), при которых бы производная достигала значений из промежутка (0;6), а он является вложенным в промежуток (-4;6).
Из этого следует, что первое условие – обязательное.
Теперь, сделав небольшие изменения в первоначальном условии, докажем, что второе условие также обязательно. Рассмотрим ту же функцию на том же промежутке, однако добавим в неравенства ещё одно условие: пусть 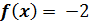 при x = 0. В таком случае, получаем, что функция на данном промежутке будет непрерывной (из определения непрерывности, так как
при x = 0. В таком случае, получаем, что функция на данном промежутке будет непрерывной (из определения непрерывности, так как  ). Другими словами, первое условие – выполняется. Однако в точке 0 производной не существует, по-прежнему, следовательно, второе условие не выполняется. Третье условие также выполняется, по всё тем же причинам. Тем не менее, для данной функции заключение теоремы – неверно, так как так как нет таких значений c є (a;b), при которых бы производная достигала значений из промежутка (0;6), а он является вложенным в промежуток (-4;6).
). Другими словами, первое условие – выполняется. Однако в точке 0 производной не существует, по-прежнему, следовательно, второе условие не выполняется. Третье условие также выполняется, по всё тем же причинам. Тем не менее, для данной функции заключение теоремы – неверно, так как так как нет таких значений c є (a;b), при которых бы производная достигала значений из промежутка (0;6), а он является вложенным в промежуток (-4;6).
Из этого следует, что второе условие является обязательным.
Если исключить условие, что A ¹ B, то теорема также потеряет смысл. Предположим обратное: пусть A = B и теорема имеет смысл. Тогда задача теоремы состоит в том, чтобы доказать, что "С є (A;B) $ c є (a;b): f’(c) = C. Рассмотрим, каких значений в таком случаем может достигать C:
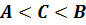 , однако, так как A = B, то составленное нами неравенство не имеет смысла и в промежутке (A;B) нет элементов, следовательно, теорема теряет смысл.
, однако, так как A = B, то составленное нами неравенство не имеет смысла и в промежутке (A;B) нет элементов, следовательно, теорема теряет смысл.
Из этого можно сделать вывод, что третье условие также является обязательным.
Замечание:
Теорема может показаться похожей на частный случай второй теоремы Больцано-Коши, однако ей не является, так как производная непрерывной функции – не всегда является непрерывной.
Применение:
· Используется в последующих разделах курса математического анализа;
Date: 2016-02-19; view: 1171; Нарушение авторских прав