
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема Ролля. Формулировка, доказательство, анализ, применение
|
|
Формулировка:
Пусть функция определена и непрерывна в [a;b], пусть существует конечная производная "x є [a;b], пусть f(a) = f(b). Тогда $ c є [a;b]: f’(c) = 0.
Доказательство:
Так как функция непрерывна в [a;b], то по 2-й теореме Вейерштрасса в [a;b] она принимает наибольшее (М) и наименьшее(m) значения.
Теперь рассмотрим два случая:
1) M = m. В таком случае, все значения функции на заданном промежутке [a;b] равны между собой, другими словами: "x є [a;b], f(x) = f(a) = f(b) = M = m. Из этого следует, что на данном отрезке функция постоянна и "x є [a;b], f’(x) = f’(a) = f’(b) = = 0, тогда такая точка с точно существует, что и требовалось доказать.
2) M > m. Для этого случая справедливо, что M є (a;b) и m є (a;b), так как в противном случае получим 1-й пример, следовательно в хотя бы одно из этих значений достигается в какой-то точке c є (a;b), а, так как из условия точки M и m – наибольшее и наименьшее значения соответственно, то по теореме Ферма: f ‘ (c) = 0, что и требовалось доказать.
Анализ:
Методы, используемые для доказательства теоремы:
· Метод дедукции;
· Перебор вариантов;
· Сведение решения задачи, к решению подзадач.
· Приведение к уже решенной задаче.
Все условия теоремы обязательны, потому как если исключить хотя бы одно из них, то теорема будет неверна. Также стоит отметить, что при невыполнении 1-го условия, не выполняется условие существования производной, соответственно не выполняется и 2-е. Обратное, однако, неверно, так как при невыполнении 2-го условия, 1-е может выполняться. Докажем обязательность условий:
1)Исключим первое условие. Может произойти две ситуации:
а) Функция будет неопределенна на всём [a;b]. В таком случае в [a;b] у функции не будет производной и теорема потеряет всякий смысл.
б) Функция будет неопределенна в конкретных точках промежутка [a;b]. В таком случае, функция будет иметь разрывы, и при попытке доказательства, не будет выполняться условие 2-й теоремы Вейерштрасса, следовательно, функция может и не достигать наименьшего и наибольшего значения, а, значит, её производная на данном отрезке может и не достигать нуля. Примером такой функции является функция: 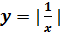 . Она определена, допустим, в промежутке
. Она определена, допустим, в промежутке
[-1; 1], за исключением точки 0, следовательно 1-е условие не выполняется. Точно также не выполняется и 2-е, как уже говорилось ранее. Третье же условие выполняется, однако при этом нет такой точки c є [a;b]: f’(c) = 0, что можно легко доказать, используя теорему Ферма:
Для начала возьмём производную от заданной функции y: 
Из теоремы Ферма следует, что если у функции есть экстремумы, то в этих точках её производная равна нулю. Проверим, при каких значениях x, функция будет обращаться в 0:

Из этого следует, что у функции нет экстремумов, что и требовалось доказать.
Следовательно, 1-е условие является необходимым.
2)Исключим второе условие. Для того чтобы выполнялось 1-е условие, но не выполнялось 2-е, достаточно, чтобы функция имела точки излома. В таком случае, производной в таких точках существовать не будет, и, если наибольшее (наименьшее) значение для функции будет достигаться в одной из точек излома, то производная в такой точке не будет достигать нуля, по той причине, что в ней производная не будет существовать.
Рассмотрим это на примере функции: 
На промежутке [-2,156338130…;-1,89396570…], (в дальнейшем для удобства:
a = -2,156338130…; b = -1,89396570…).
Действительно, на данном промежутке, функция определена и непрерывна, более того
f(a) = f(b), следовательно 3-е условие также выполняется. Кроме того, на данном промежутке также находится и излом, в точке x = -2, причём в данной точке функция достигает наибольшего значения на данном промежутке (y = 2). Теперь же легко доказать, что нет такой точки c є [a;b]: f’(c) = 0, используя теорему Ферма:
Для начала возьмём производную от заданной функции y:
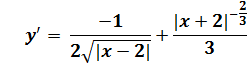
Теперь попробуем найти точки, в которых производная равна нулю:
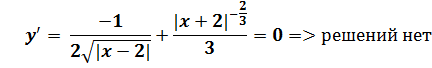
Таким образом, не смотря на то, что функция имеет наибольшее значение, производная в нуль не обращается.
Из этого следует, что 2-е условие – обязательное.
3)Исключим третье условие. Для того, чтобы доказать, что условие необходимо, приведём пример функции, для которой выполняется условие (1) и (2), но невозможно выделить такие a и b, чтобы выполнилось 3-е условие. Примером такой функции является функция: 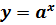 .
.
Действительно, область определения данной функции – множество всех вещественных чисел; на всей области определения функция имеет конечную производную; для данной функции невозможно выделить такие a и b, чтобы выполнилось 3-е условие, так как она монотонно возрастает. Другими словами, 1-е и 2-е условия выполняются всегда, а 3-е – никогда.
Теперь попробуем найти такую точку c є R: f’(c) = 0. Для начала возьмём производную от заданной функции y: 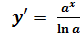 . Из теоремы Ферма следует, что если у функции есть экстремумы, то в этих точках её производная равна нулю. Проверим, при каких значениях x, функция будет обращаться в 0:
. Из теоремы Ферма следует, что если у функции есть экстремумы, то в этих точках её производная равна нулю. Проверим, при каких значениях x, функция будет обращаться в 0:

Из этого следует, что у функции нет экстремумов, что и требовалось доказать.
Следовательно, условие 3 является обязательным.
Применение:
· Используется для доказательства теоремы Лагранжа;
· Является частным случаем теоремы Лагранжа;
· Существует также 2 следствия:
1) Если дифференцируемая функция обращается в ноль в  различных точках, то ее производная обращается в ноль, по крайней мере, в
различных точках, то ее производная обращается в ноль, по крайней мере, в 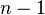 различных точках, причем эти нули производной лежат в выпуклой оболочке нулей исходной функции.
различных точках, причем эти нули производной лежат в выпуклой оболочке нулей исходной функции.
2) Дифференцируемая функция на отрезке между двумя своими точками имеет касательную, параллельную секущей/хорде, проведённой через эти две точки.
Date: 2016-02-19; view: 1406; Нарушение авторских прав