
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения типовых задач. Пример 1. Найти общее решение уравнения и частное решение, удовлетворяющее начальному условию
|
|
Пример 1. Найти общее решение уравнения 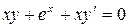 и частное решение, удовлетворяющее начальному условию
и частное решение, удовлетворяющее начальному условию  .
.
Решение. Перепишем данное уравнение так:  - и рассмотрим однородное уравнение
- и рассмотрим однородное уравнение  . Так как
. Так как  (значение
(значение  не является решением неоднородного уравнения), то
не является решением неоднородного уравнения), то

- общее решение однородного уравнения.
Применяем далее метод вариации произвольной постоянной  . Общее решение неоднородного уравнения будем искать в виде
. Общее решение неоднородного уравнения будем искать в виде  ;
;  . Подставив значения
. Подставив значения  и
и  в неоднородное уравнение, получим
в неоднородное уравнение, получим
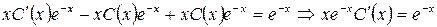 .
.
Так как  , то
, то
 .
.
Подставив это значение  в общее решение неоднородного уравнения, по лучим
в общее решение неоднородного уравнения, по лучим  - общее решение неоднородного уравнения.
- общее решение неоднородного уравнения.
Для нахождения частного решения подставим значения  ,
,  в общее решение:
в общее решение:  . Значит,
. Значит,  - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
Пример 2. Найти общее решение уравнения 2ху"' = у" и частное решение, удовлетворяющее начальным условиям  ,
,  ,
,  .
.
Решение. Пусть  .
.
Имеем 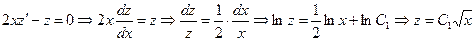 .
.
Но  ;
; 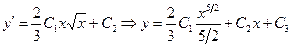 .
.
Следовательно,  - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
Чтобы найти частное решение, подставим в выражения для  ,
,  и
и  значение
значение  :
:
 ;
;
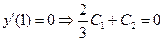 ;
;
 .
.
Из системы уравнений  ;
;  находим
находим  ;
; 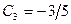 . Значит, искомое частное решение имеет вид
. Значит, искомое частное решение имеет вид
 .
.
Пример 3. Найти общее решение уравнения  и частное решение, удовлетворяющее начальным условиям
и частное решение, удовлетворяющее начальным условиям 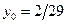 ;
; 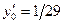 .
.
Решение. Рассмотрим однородное уравнение  . Соответствующее характеристическое уравнение имеет вид
. Соответствующее характеристическое уравнение имеет вид  , откуда
, откуда 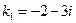 ,
,  . Следовательно,
. Следовательно,  общее решение однородного уравнения.
общее решение однородного уравнения.
Частное решение неоднородного уравнения будем искать в виде  . Имеем
. Имеем
 ,
,  .
.
Подставим эти выражения в неоднородное уравнение
 ;
;

и получим систему для вычисления коэффициентов А и В:
 .
.
Итак, частное решение неоднородного уравнения имеет вид
 ,
,
а общее решение неоднородного уравнения – вид
 .
.
Найдем частное решение, удовлетворяющее заданным начальным условиям:
 ;
;
 ;
;
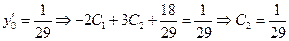 .
.
Искомое частное решение таково:
 .
.
Пример 4. Найти общее решение системы
 .
.
Решение. Перепишем систему в виде
 .
.
Рассмотрим характеристическое уравнение:
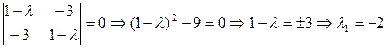 ;
;  .
.
Подставим найденные значения корней характеристического уравнения в систему линейных алгебраических уравнений относительно  ,
, 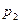 .
.
Для  имеем
имеем
 ;
;
(второе уравнение есть следствие первого). Возьмем, например,  ; тогда
; тогда  . Полагая
. Полагая  , найдем
, найдем  ;
;  . Итак, для
. Итак, для  получим
получим 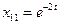 ;
;  .
.
Для 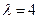 имеем
имеем
 ;
;
(второе уравнение есть следствие первого). Возьмем, например,  ; тогда
; тогда  . Полагая
. Полагая  , найдем
, найдем  ;
;  . Итак, для
. Итак, для 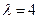 получим
получим  ;
;  .
.
Фундаментальная система решений:
для  :
: 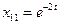 ;
;  .
.
для 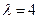 :
:  ;
;  .
.
Следовательно, общее решение системы имеет вид
 ;
;  .
.
Пример 5. Дана струна, закрепленная на концах  ,
,  . Пусть в начальный момент времени форма струны имеет вид ломаной
. Пусть в начальный момент времени форма струны имеет вид ломаной  , изображенной на рис. 5.
, изображенной на рис. 5.

Рис. 5
Найти форму струны для любого момента времени, если

Решение. Из рисунка и условия задачи имеем

Находим
 .
.
Интеграл  берем по частям;
берем по частям;  ,
,  , откуда
, откуда  ,
,  ; следовательно;
; следовательно;
 .
.
Итак,

Окончательно, получим  . Далее, находим
. Далее, находим
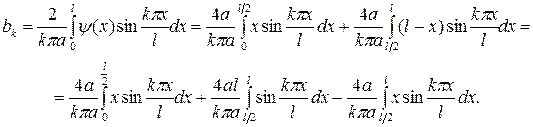
Окончательно получим 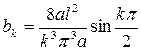 .Таким образом, искомая функция имеет вид:
.Таким образом, искомая функция имеет вид:
 .
.
4.3. Контрольная работа №7
Задача №35.
Найти общее решение дифференциального уравнения и выделить частное решение, удовлетворяющее начальному условию.
| Номер варианта | 
| Начальное условие |

| 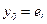 
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |
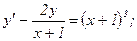
|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |
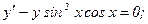
|  
|
Задача №36.
Найти общее решение дифференциального уравнения и выделить частное решение, удовлетворяющее начальным условиям.
| Номер варианта | 
| Начальное условие |

| 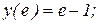 
| |

|   
| |

|  
| |

|  
| |

|  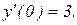
| |

|  
| |

| 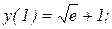 
| |

|   
| |

|  
| |

|   
| |

|  
| |

|  
| |

| 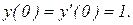
| |

| 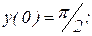 
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
| |

|  
|
Задача №37
Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям ( ).
).
| Номер варианта | 
| Начальное условие |

|   
| |

|   
| |

| 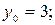 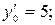 
| |

|   
| |

|   
| |

| 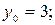  
| |

| 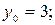  
| |

|   
| |

|   
| |

|   
| |

|   
| |

|   
| |

|   
| |

|   
| |

|  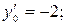 
| |

|   
| |

|  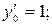 
| |

|   
| |
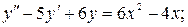
|   
| |

|  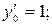 
|
Задача №38.
Найти общее решение системы дифференциальных уравнений.
| Номер варианта | Система | Номер варианта | Система | Номер варианта | Система |

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
|
Задача №39
Решить уравнение колебаний струны методом Фурье.
| Номер варианта | 
| 
|
 
|  
| |
 
|  
| |
 
|   ; ;
| |
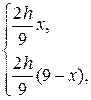 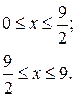
|  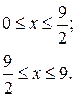
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
| 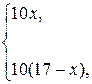 
| |
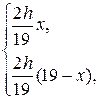 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
| |
 
|  
|
Вопросы к экзамену
1. Сформулируйте теорему о существовании и единственности решения дифференциального уравнения.
2. Изложите метод решения дифференциального уравнения вида 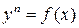 . Приведите пример.
. Приведите пример.
3. Изложите метод решения дифференциального уравнения вида  . Приведите пример.
. Приведите пример.
4. Изложите метод решения дифференциального уравнения вида  . Приведите пример.
. Приведите пример.
5. Дайте определение линейного дифференциального уравнения  -го порядка (однородного и неоднородного).Докажите основные свойства частных решений линейного однородного дифференциального уравнения.
-го порядка (однородного и неоднородного).Докажите основные свойства частных решений линейного однородного дифференциального уравнения.
6. Дайте определение линейно зависимых и линейно независимых функций и приведите примеры. Докажите, что для линейно зависимых функций определитель Вронского равен нулю. Сформулируйте обратную теорему для линейно независимых решений (интегралов) однородного дифференциального уравнения.
7. Докажите теорему об общем решении линейного однородного дифференциального уравнения.
8. Изложите метод нахождения общего решения линейного однородного дифференциального уравнения второго порядка, если известно одно его частное решение. Приведите пример.
9. Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения. Приведите пример.
10. Выведите формулу общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае равных корней характеристического уравнения. Приведите пример.
11. Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. Приведите пример.
12. Докажите теорему об общем решении линейного неоднородного дифференциального уравнения второго порядка.
13. Докажите, что сумма частных решений уравнений 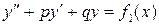 и
и  является решением уравнения
является решением уравнения 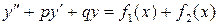 .
.
14. Изложите правило нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида  , где
, где  - многочлен степени
- многочлен степени  .
.
15. Изложите правило нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида 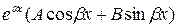 .
.
16. Что называется нормальной системой дифференциальных уравнений первого порядка? Сформулируйте задачу Коши для этой системы.
17. Изложите методы нахождения общего решения нормальной системы двух линейных однородных дифференциальных уравнений с постоянными коэффициентами.
18. Выведите уравнение колебаний струны. Сформулируйте краевую задачу о колебаниях струны, закреплённой на концах.
19. Изложите метод Даламбера нахождения решения задачи Коши о колебаниях бесконечной струны.
20. Изложите метод Фурье нахождения решения краевой задачи о колебаниях струны, закреплённой на концах.
5. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Л и т е р а т у р а: [4]. т. 2, гл. XX; [5], гл. XVIII.
Date: 2016-02-19; view: 821; Нарушение авторских прав