
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные теоретические сведения. 1.Общим решением дифференциального уравнения первого порядка называется дифференцируемая функция , которая при любом значении произвольной постоянной С
|
|
1.Общим решением дифференциального уравнения первого порядка называется дифференцируемая функция 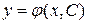 , которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения
, которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения 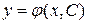 при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям
при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям  при
при  (другая запись:
(другая запись:  ), называется задачей Коши.
), называется задачей Коши.
График всякого решения  данного дифференциального уравнения, построенный на плоскости
данного дифференциального уравнения, построенный на плоскости  , называется интегральной кривой этого уравнения.
, называется интегральной кривой этого уравнения.
2.Уравнение вида 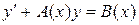 называется линейным. Если
называется линейным. Если  ,то уравнение называется однородным; если
,то уравнение называется однородным; если 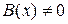 –неоднородным. Общее решение однородного уравнения получается путем разделения переменных; общее решение неоднородного уравнения получается из общего решения соответствующего однородного уравнения с помощью вариации произвольной постоянной интегрирования С.
–неоднородным. Общее решение однородного уравнения получается путем разделения переменных; общее решение неоднородного уравнения получается из общего решения соответствующего однородного уравнения с помощью вариации произвольной постоянной интегрирования С.
Данное неоднородное уравнение можно интегрировать также с помощью замены  , где
, где  – две неизвестные функции.
– две неизвестные функции.
3.Дифференциальное уравнение  –го порядка, разрешенное относительно, производной, имеет вид
–го порядка, разрешенное относительно, производной, имеет вид 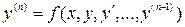 .
.
Задача нахождения решения  данного уравнения, удовлетворяющего начальным условиям
данного уравнения, удовлетворяющего начальным условиям  ,
,  называется задачей Коши.
называется задачей Коши.
Для нахождения частного решения иногда используют так называемые краевые условия. Эти условия (их число не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка. Краевые условия ставятся лишь для уравнений порядка выше первого.
4. Теорема существования и единственности решения задачи Коши. Если в уравнении  функция
функция  :
:
а) непрерывна по всем своим аргументам  в некоторой области
в некоторой области  их изменения; б) имеет ограниченные в области
их изменения; б) имеет ограниченные в области  частые производные,
частые производные,  по аргументам
по аргументам  , то найдется интервал
, то найдется интервал 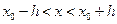 , на котором существует единственное решение
, на котором существует единственное решение  данного уравнения, удовлетворяющее условиям
данного уравнения, удовлетворяющее условиям 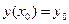 ;
;  ; …;
; …;  , где значения
, где значения  ;
;  ;
;  ; …;
; …;  содержатся в области D.
содержатся в области D.
Проинтегрировать (в конечном виде) уравнение n-го порядка можно только в некоторых частных случаях.
5. Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид  , где
, где 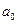 ,
,  ,
,  - числа, причем
- числа, причем  . Если
. Если  , то уравнение называется однородным, а если
, то уравнение называется однородным, а если 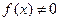 - неоднородным.
- неоднородным.
6. Квадратное уравнение  называется характеристическим уравнением дифференциального уравнения
называется характеристическим уравнением дифференциального уравнения  . Пусть
. Пусть  - дискриминант квадратного уравнения. Возможны следующие случаи:
- дискриминант квадратного уравнения. Возможны следующие случаи:
1)  - общим решением уравнения
- общим решением уравнения  является функция
является функция  (
(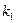 и
и  - корни характеристического уравнения);
- корни характеристического уравнения);
2)  - общим решением служит функция
- общим решением служит функция  , (
, ( - корень характеристического уравнения),
- корень характеристического уравнения),
3)  - общим решением является
- общим решением является  , (
, ( ,
,  - корни характеристического уравнения).
- корни характеристического уравнения).
7. Решение неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами основывается на следующей теореме.
Теорема. Если  - некоторое частное решение неоднородного уравнения
- некоторое частное решение неоднородного уравнения  и
и 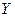 - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения  , то общее решение неоднородного уравнения имеет вид
, то общее решение неоднородного уравнения имеет вид  .
.
Укажем правило нахождения частного решения неоднородного уравнения методом неопределенных коэффициентов.
1) Пусть  ; тогда:
; тогда:
а)  , если нуль не является корнем характеристического уравнения;
, если нуль не является корнем характеристического уравнения;
б)  , если нуль является простым корнем характеристического уравнения;
, если нуль является простым корнем характеристического уравнения;
в)  , если нуль является двукратным корнем характеристического уравнения.
, если нуль является двукратным корнем характеристического уравнения.
2) Пусть 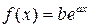 ; тогда:
; тогда:
а)  , если число
, если число  не является корнем характеристического уравнения,
не является корнем характеристического уравнения,
б)  , если число
, если число  является корнем характеристического уравнения,
является корнем характеристического уравнения,
в)  , если число
, если число  является двукратным корнем характеристического уравнения.
является двукратным корнем характеристического уравнения.
3) Пусть  ; тогда:
; тогда:
а) 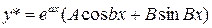 , если число
, если число  не является корнем
не является корнем
характеристического уравнения;
б)  , если число
, если число  является корнем характеристического уравнения;
является корнем характеристического уравнения;
8. Система дифференциальных уравнений вида

где  неизвестные функции независимой переменной
неизвестные функции независимой переменной  , называется нормальной системой.
, называется нормальной системой.
Пусть дана система  линейных дифференциальных уравнений с постоянными коэффициентами:
линейных дифференциальных уравнений с постоянными коэффициентами:

Эту систему можно записать в виде одного матричного дифференциального уравнения  , где
, где
 ;
;  ;
; 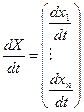 .
.
Решение системы ищем в виде  ,
,  ,
,  . Подставив значения
. Подставив значения  ,
,  , …,
, …, 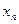 в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно
в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно  ,
, 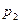 , …,
, …,  :
:

Система должна иметь ненулевое решение, поэтому для определения  полу чаем уравнение
полу чаем уравнение  -й степени:
-й степени:

Пусть это характеристическое уравнение имеет  различных корней
различных корней  ,
, 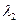 , …,
, …,  . Тогда система дифференциальных уравнений имеет
. Тогда система дифференциальных уравнений имеет  решений:
решений:
1-е решение, соответствующее корню  :
:
 ;
;  ; …;
; …;  ;
;
2-е решение, соответствующее корню  :
:
 ;
; 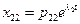 ; …;
; …;  ;
;
 -е решение, соответствующее корню
-е решение, соответствующее корню  :
:
 ;
;  ; …;
; …;  .
.
Получена фундаментальная система решений. Общее решение системы имеет вид

9. Пусть  - функция, характеризующая отклонение точек струны от положения равновесия в момент времени
- функция, характеризующая отклонение точек струны от положения равновесия в момент времени  . Функция
. Функция  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению
 ;
;
где 
 ,
,  - масса единицы длины (линейная плотность струны);
- масса единицы длины (линейная плотность струны);  - сила, действующая на струну перпендикулярно оси
- сила, действующая на струну перпендикулярно оси  и рассчитанная на единицу длины;
и рассчитанная на единицу длины; 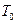 - начальное натяжение.
- начальное натяжение.
Если  (т. е. внешняя сила отсутствует), то получается уравнение свободных колебаний струны
(т. е. внешняя сила отсутствует), то получается уравнение свободных колебаний струны 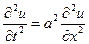 . Пусть
. Пусть  ,
, 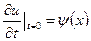 (форма и скорость струны в начальный момент времени). Эти условия называются начальными условиями задачи.
(форма и скорость струны в начальный момент времени). Эти условия называются начальными условиями задачи.
Решение дифференциального уравнения свободных колебаний струны имеет вид:
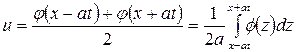 .
.
Решение дифференциального уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ;
;  и граничным (краевым) условиям
и граничным (краевым) условиям  и
и  , может быть представлено как сумма бесконечного ряда:
, может быть представлено как сумма бесконечного ряда:
 ,
,
где 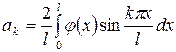 ,
,  .
.
Граничные условия вводятся при изучении колебании струны длины  , закрепленной в двух точках
, закрепленной в двух точках  и
и  .
.
Date: 2016-02-19; view: 817; Нарушение авторских прав