
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения типовых задач. Пример 1. Исследовать на сходимость числовой ряд
|
|
Пример 1. Исследовать на сходимость числовой ряд

Решение. Проверяем сходимость ряда по признаку Даламбера (3). Так как общий член ряда  то заменяя в выражении n-го члена n на n+1, находим
то заменяя в выражении n-го члена n на n+1, находим  Затем ищем предел отношения последующего члена
Затем ищем предел отношения последующего члена  к предыдущему
к предыдущему  при
при  :
:
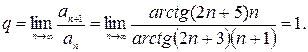
Поскольку полученный предел равен единице, признак Даламбера не дает ответа на вопрос о сходимости ряда (здесь для вычисления предела было использовано правило Лопиталя). Применим теперь признак сравнения в предельной форме. В качестве эталонного ряда выберем ряд  и в силу формулы (2) получим
и в силу формулы (2) получим

Следовательно, исследуемый ряд является расходящимся, так как эталонный ряд с общим членом 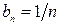 расходится (гармонический ряд).
расходится (гармонический ряд).
Пример 2. Найти радиус и интервал сходимости степенного ряда  Исследовать сходимость ряда на концах интервала сходимости.
Исследовать сходимость ряда на концах интервала сходимости.
Решение. Радиус сходимости находим по формуле (6):

Интервал сходимости данного ряда определяется неравенством  или
или  .
.
Исследуем концы интервала сходимости. При x= -1 получаем числовой ряд

расходимость которого может быть установлена с помощью предельного признака сравнения (эталонный ряд – гармонический).
При x= -3 получаем числовой знакочередующийся ряд

который сходится по признаку Лейбница. Так как ряд, составленный из абсолютных членов данного ряда, т.е. ряд  расходится, то исследуемый ряд сходится условно.
расходится, то исследуемый ряд сходится условно.
Таким образом, интервал сходимости исследуемого степенного ряда имеет вид 
Пример 3. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение. Разложим подынтегральную функцию в биномиальный ряд по степеням x:
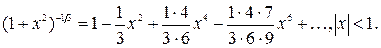
Так как отрезок интегрирования [-0.6;0] находится внутри интервала сходимости биноминального ряда, то ряд можно почленно интегрировать. Подставляя в интеграл, вышеприведенное разложение подынтегральной функции и почленно интегрируя в указанных пределах, получаем


Четвертый член  меньше 0.001. Поэтому согласно неравенству (4) для вычисления приближенного значения интеграла с требуемой точностью достаточно ограничиться первыми тремя членами ряда:
меньше 0.001. Поэтому согласно неравенству (4) для вычисления приближенного значения интеграла с требуемой точностью достаточно ограничиться первыми тремя членами ряда:

Пример 4. Найти сумму ряда с комплексными членами:

Решение. Общий член данного ряда имеет вид

т.е. ряд, по определению, является функцией  при
при  [см. формулу (7)]. Следовательно, сумма этого ряда равна значению функции
[см. формулу (7)]. Следовательно, сумма этого ряда равна значению функции  в указанной точке:
в указанной точке: 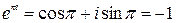 [см. формулу (8)]. Таким образом, получаем
[см. формулу (8)]. Таким образом, получаем 
Пример 5. Разложить периодическую функцию  в ряд Фурье по косинусам.
в ряд Фурье по косинусам.
Решение. Данная функция определена на полупериоде [0,3], т.е. l=3. Для разложения такой функции в ряд Фурье по косинусам ее следует продолжить на второй полупериод [-3,0) четным образом (рис. 4).

Рис. 4
Для четной функции коэффициенты bn=0, а коэффициенты  вычисляются по формулам (9):
вычисляются по формулам (9):

 |

 при x³1,
при x³1,
при x<1,
то отрезок интегрирования разобьем на два отрезка: от 0 до 1, где  и от 1 до 3, где
и от 1 до 3, где  Тогда
Тогда

При n=0 имеем

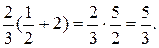
Для вычисления коэффициентов  (n=1,2,…) применим метод интегрирования по частям:
(n=1,2,…) применим метод интегрирования по частям:
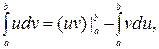
причем в первом интеграле примем u=1- x, 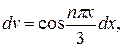 откуда du= -dx,
откуда du= -dx,  Во втором интеграле положим
Во втором интеграле положим 
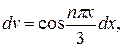 откуда
откуда
du=dx,  Тогда
Тогда
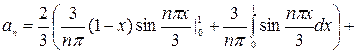



так как 
 Следовательно, искомое разложение функции в ряд Фурье по косинусам имеет вид
Следовательно, искомое разложение функции в ряд Фурье по косинусам имеет вид

Это разложение справедливо в области непрерывности данной функции.
3.2. Контрольная работа № 6
Задача №30
Исследовать сходимость числовых рядов  .
.
| № | Общий член ряда 
|
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в) 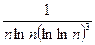 ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а) 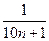 ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б) 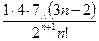 ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
| |
а) 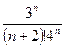 ; б) ; б)  ; в) ; в) 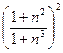 ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 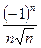
| |
а)  ; б) ; б)  ; в) ; в) 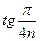 ; г) ; г) 
| |
а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 
|
Задача №31
Найти интервал сходимости степенного ряда  . Исследовать сходимость ряда на концах интервала.
. Исследовать сходимость ряда на концах интервала.
| № | Коэффициент 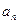
| № | Коэффициент 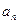
|
а)  ; б) ; б) 
| а)  ; б) ; б) 
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 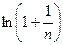
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 
| ||
а)  ; б) ; б) 
| а) 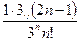 ; б) ; б) 
| ||
а)  ; б) ; б) 
| а)  ; б) ; б) 
|
Задача №32
Вычислить определенный интеграл  с точностью до 0,001 путем разложения подынтегральной функции в степенной ряд и почленного интегрирования полученного ряда.
с точностью до 0,001 путем разложения подынтегральной функции в степенной ряд и почленного интегрирования полученного ряда.
| № | Функция f(x), b | № | Функция f(x), b |
 ; 1 ; 1
| 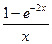 ; 0,1 ; 0,1
| ||
 ; 0,5 ; 0,5
|  ; 1,5 ; 1,5
| ||
 ; 1 ; 1
|  ; 1 ; 1
| ||
 ; 0,5 ; 0,5
|  ; 0,2 ; 0,2
| ||
 ; 0,1 ; 0,1
|  ; 1 ; 1
| ||
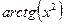 ; 0,75 ; 0,75
|  ; 1 ; 1
| ||
 ; 0,5 ; 0,5
|  ; 1 ; 1
| ||
 ; 0,1 ; 0,1
|  ; 0,1 ; 0,1
| ||
 ; 0,5 ; 0,5
|  ; 0,1 ; 0,1
| ||
 ; 0,5 ; 0,5
|  ; 0,4 ; 0,4
|
Задача №33
Найти три первых, отличительных от нуля, члена разложения в степенной ряд решение  дифференциального уравнения
дифференциального уравнения 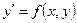 , удовлетворяющего условию
, удовлетворяющего условию  .
.
| № | 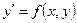 ; ; 
| № | 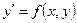 ; ; 
|
 ; ;  =1 =1
|  ; ;  =0,1 =0,1
| ||
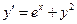 ; ;  =0 =0
|  ; ;  =1 =1
| ||
 ; ;  =3 =3
|  ; ;  =1 =1
| ||
 ; ;  =0 =0
|  ; ;  =1 =1
| ||
 ; ;  =1 =1
|  ; ;  =0,1 =0,1
| ||
 ; ;  =4 =4
|  ; ;  =0 =0
| ||
 ; ;  =2 =2
|  ; ;  =0 =0
| ||
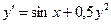 ; ;  =1 =1
|  ; ;  =2 =2
| ||
 ; ;  =0 =0
|  ; ;  =1 =1
| ||
 ; ;  =5 =5
|  ; ;  =0 =0
|
Задача №34
Разложить в ряд Фурье периодическую функцию, заданную на полупериоде 
 по синусам или по косинусам. Построить график функции и график суммы полученного ряда Фурье.
по синусам или по косинусам. Построить график функции и график суммы полученного ряда Фурье.
| № | 
|
 по косинусам по косинусам
| |
  по синусам по синусам
| |
  по косинусам по косинусам
| |
 по синусам по синусам
| |
 по косинусам по косинусам
| |
 по синусам по синусам
| |
 по косинусам по косинусам
| |
 по синусам по синусам
| |
 по косинусам по косинусам
| |
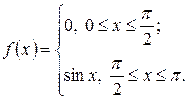 по синусам по синусам
| |
 по синусам по синусам
| |
 по косинусам по косинусам
| |
 по синусам по синусам
| |
 по косинусам по косинусам
| |
 ; ;  по синусам по синусам
| |
 по косинусам по косинусам
| |
 по синусам по синусам
| |
 по косинусам по косинусам
| |
 по синусам по синусам
| |
 по косинусам по косинусам
|
Вопросы к экзамену
1. Дайте определения сходящегося и расходящегося рядов. Докажите необходимый признак сходимости ряда.
2. Докажите, что отбрасывание конечного числа членов ряда не изменяет его сходимости (расходимости). Покажите, что сумма ряда равна сумме первых его  членов, сложенной с суммой ряда, полученного из данного отбрасыванием этих
членов, сложенной с суммой ряда, полученного из данного отбрасыванием этих  членов.
членов.
3. Докажите теорему о сравнении рядов с положительными членами.
4. Докажите признак Деламбера сходимости знакопостоянных рядов.
5. Докажите интегральный признак сходимости ряда (Коши). Приведите примеры на применение этого признака.
6. Дайте определение абсолютно сходящегося ряда. Докажите, что из абсолютной сходимости ряда следует его сходимость. Сформулируйте свойства абсолютно сходящихся рядов.
7. Докажите признак Лейбница сходимости знакочередующихся рядов. Покажите, что при замене суммы ряда типа Лейбница суммой первых его  членов допускаемая абсолютная погрешность не превосходит модуля первого отброшенного члена.
членов допускаемая абсолютная погрешность не превосходит модуля первого отброшенного члена.
8. Дайте определение области сходимости функционального ряда. Приведите примеры рядов с различными областями сходимости.
9. Докажите теорему Абеля о сходимости степенных рядов.
10. Выведите формулу для вычисления радиуса сходимости степенного ряда.
11. Выведите условия разложимости функции в ряд Тейлора.
12. Сформулируйте теоремы об интегрировании и дифференцировании степенных рядов.
13. Изложите метод приближённого вычисления определённых интегралов с помощью рядов.
14. В чём состоит задача численного интегрирования дифференциального уравнения?
15. Изложите метод Эйлера и метод Адамса численного интегрирования дифференциального уравнения.
16. Изложите метод приближённого интегрирования дифференциальных уравнений с помощью степенных рядов.
17. Выведите формулы для коэффициентов ряда Фурье.
18. Сформулируйте достаточные условия разложимости функции в ряд Фурье.
19. Выведите формулы для коэффициентов ряда Фурье для чётных и нечётных функций.
20. Представьте ряд Фурье в комплексной форме.
Date: 2016-02-19; view: 2091; Нарушение авторских прав