Зависимости степенного типа

Уравнение вида y=b₀+b₁x+b₂x² приводится к линейному виду заменой x²=Z в результате чего получаем зависимость y=b₀+b₁x+b₂Z. В общем случае для полинома k-той степени y=b₀+b₁x+b₂x²+…+b_kx^k выполняются замена x²=Z₁,…,x³=Z₂,…,x^k=Z_k-1.

Зависимость вида 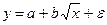линеаризуется путем замещения .

В общем случае степенная зависимость вида приводится к линейному виду путем логарифмирования обеих частей уравнения 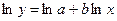соответственно заменяется lny=Z, lna=A, lnx=S и находят параметры уравнения Z=A+Sb+ .

Приведенные примеры не исчерпывают классических линеарных уравнений. Аналогично могут быть линеаризированы и другие функции. При этом после линеаризации функция должна иметь линейный вид относительно коэффициентов уравнения. Основной практической трудностью является выбор того или иного типа зависимости.

2. Регрессионное уравнение используется для решения многих задач экономических исследований, но наиболее важным из них является прогнозирование. В частности, без регрессионных моделей невозможно построение так называемых сценарных подходов, которые в общем случае отвечают на вопрос «что будет, если…»

После получения адекватных регрессионных уравнений прогнозирование осуществляется путем подстановки в регрессионное уравнение прогнозного значения независимых переменных, то есть прогнозное значение у определяется как функция:

y_прог=f(x_{прогноз}).

Таким образом, для прогнозирования на основе регрессионных уравнений основной задачей является получение адекватных уравнений.

Существенным вопросом при прогнозировании является вопрос надежности прогноза, который в свою очередь сводится к проблеме построения доверительных интервалов прогноза. Построение доверительных интервалов прогноза для однофакторного уравнения опирается на оценку дисперсии ошибки прогноза.

где x_Т – значение независимой переменной, для которого определяется прогноз;

- остаточная дисперсия регрессионного уравнения;

Используя можно построить доверительный интервал для истинного значения прогноза y_Т с заданной вероятностью. Для этого рассчитывается величина t по формуле:

которая подчиняется t- распределению с n-2 степенями свободы.

Отсюда с заданной вероятностью величина t находится в интервале:

Отсюда интервал для истинного значения прогноза определяется как:

Таким образом, ширина доверительного интервала прогноза зависит от следующих характеристик:

1. С ростом остаточной дисперсии уравнения регрессии - ширина доверительного интервала увеличивается, то есть чем лучше качество подгонки регрессионного уравнения, тем надежнее прогноз.

2. С расширением выборки (с ростом n) доверительный интервал прогноза сужается, то есть чем больше информации используется в предпрогнозных исследованиях, тем точнее прогноз.

3. С удалением прогнозного значения аргумента от среднего значения выборки ширина доверительного интервала прогноза увеличивается. Это объясняется тем обстоятельством, что с отдалением прогнозного периода неопределенность прогноза увеличивается.

Ширина доверительного интервала зависит также от значений t-статистики, который в свою очередь зависит от заданной вероятности p. С увеличением вероятности при прочих равных условиях t-статистика увеличивается, а интервал расширяется.

Date: 2016-02-19; view: 694; Нарушение авторских прав