Учет качественных факторов

Теория эконометрики не накладывает никаких ограничений на характер объясняющих переменных в той части, что они могут быть и непрерывными и дискретными величинами. Это обстоятельство дает возможность решить проблему учета влияния качественных факторов через определения специальных переменных, описывающих влияние качественных факторов. Такие переменные называются качественными. Оценка таких переменных может быть осуществлена на базе экспертных оценок. Данные о качестве объекта или явления могут быть собраны у экспертов в 3 формах.

Первая форма представления данных – балльная оценка качественного показателя. В данном случае данные собираются в виде матрицы.

где Х_nm – оценка качества объекта, полученного от j-го эксперта;

n – число оценочных объектов;

m – число экспертов.

Вторая форма представления данных – экспертное упорядочивание, которое предполагает ранжирование обследуемых объектов по степени проявления в них анализируемого свойства.

где К_mn – место присвоенное j-му объекту j-тым экспертом (K_ij).

Третья форма – формирование булевой матрицы парных сравнений по правилам:

X_ik,j=

После сбора экспертной оценки одним из методов вычисляется свободный показатель (качественная переменная).

В дальнейшем на стадии моделирования, полученные таким образом качественные переменные, учитываются либо путем прямого включения в модель, либо с помощью специальных моделей.

Нелинейные регрессионные модели и использование регрессионных моделей для прогнозирования

1. Нелинейные регрессионные модели.

2. Использование для прогнозирования.

1. Пусть Y и X₁,X₂,_…,X_n соответственно результирующая и объясняющие переменные. А – случайная компонента. Рассмотрим из всех видов нелинейных моделей класс линеализуемых, то есть приводящихся к линейному виду с помощью тех или иных преобразований.

Зависимости гиперболического типа.

Предположим, что исследуемые переменные и случайные регрессионные остатки связаны между собой статистической связью вида:

( <x< )

Соответствующая кривая регрессии характеризуется двумя асимптотами:

Горизонтальной у=a, и вертикальной x=0

y

b>0

x

b<0

В модели такого вида линеализируются путем замены переменной 1/x=z и с помощью метода наименьших квадратов находят параметры уравнения у=a+bz+ .

В случае, когда у, x, представлены зависимостью вида:

Переход к линейной модели осуществляется заменой u= и решается уравнение

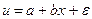
Зависимости показательного (экспоненциального) типа. Достаточно широкий класс экономических показателей характеризуется приблизительно постоянным темпом относительного прироста по времени. Этому соответствует следующая форма зависимости

b<0 b>0

В данном случае перейти к линейной форме зависимости можно прологарифмировав обе части уравнения:

lny=lna+bx

Далее делается подстановка:

lny=z, lna=A и находятся параметры z=A+bx.

Част случай экспоненциальной зависимости является так называемая логическая кривая, которая имеет следующее уравнение:

()

Данная кривая имеет 2 горизонтальные асимптоты у=0 и у=1/а

Логистические кривые используются для описания поведения показателей, имеющих определенные уровни насыщения. Например, для описания зависимости спроса на товар от дохода. Линеаризация происходит с помощью замены:

, и решаем уравнение

Зависимости логарифмического типа.

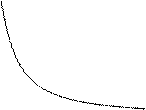
Зависимости вида y=a+blnx+ (0<x< ) имеют в качестве вертикальной асимптоты оси y и линеаризуются путем замены lnx=S и решаем уравнение y=a+bS+

b>0

a

b<0

Date: 2016-02-19; view: 452; Нарушение авторских прав