Частотні критерії стійкості

Один з частотних критеріїв був запропонований в 1932 р. американським фізиком Х.Найквістом, який досліджував властивості електронних підсилювачів із зворотніми зв’язками. Цей критерій потім став одним з найбільш уживаних при дослідженнях стійкості автоматичних систем.

На відміну від інших критеріїв, заснованих на аналізі характеристичного рівняння системи, цей критерій використовує амплітудно-фазову характеристику розімкненої системи , тобто послідовне з’єднання (добуток) відповідних характеристик і передаточних функцій автоматичного регулятора і об’єкта по каналу керування. Саме це забезпечує наочність та зручність використання критерія, можна застосовувати експериментальні динамічні характеристики об’єкта. Цей критерій особливо зручний для одноконтурних систем, які можна представити у вигляді типових ланок.

Основне застосування критерія Найквіста відноситься до систем, які є стійкими в розімкненому стані, що виконується в більшості випадків для технологічних об’єктів. Для цього випадку критерій Найквіста формулюється так: автоматична система керування стійка, якщо амплітудно-фазова характеристика розімкненої системи 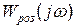не охоплює точку з координатами (-1; j0) (рис.4.3).

ω=0

ω=

Рис.4.3. Амплітудно-фазові характеристики розімкненої системи (статичної)

Годограф 1 відповідає стійкій системі, 3 – нестійкій, 2 – на межі стійкості. Цей випадок справедливий для статичних систем. Для астатичних систем відповідні характеристики наведені на рис.4.4.

ω=0

Рис.4.4. Амплітудно-фазові характеристики розімкненої системи (астатичної)

При подальшому аналізі використовуються такі значення частоти:

- частота зрізу, коли А(ω) (модуль ;

- частота, при якій фазовий зсув .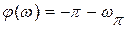

Тоді умова знаходження системи на межі стійкості буде:

(4.24)

Якщо проаналізувати проходження гармонійного сигнала через систему, то роль особливої точки (-1; j0) полягає в тому, що:

- вона відповідає претворенню від’ємного зворотнього зв’язку в додатній;

- вона є межею між режимами підсилення і ослаблення зовнішнього сигналу системою.

Може бути випадок, коли системи є нестійкою, в розімкненому стані. Тоді критерій Найквіста формулюється так: АСР буде стійкою, коли 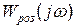охоплює /2 разів точку з координатами (-1; j0), - число правих коренів характеристичного рівняння розімкненої системи.

Критерій Найквіста зручно використовувати для аналіза систем, які мають в своїй структурі ланки запізнювання. В цьому випадку АФХ розімкненої системи можна подати у вигляді:

, (4.25)

де: - АФХ основних елементів системи;

- АФХ ланки запізнювання.

Наявність ланки запізнювання погіршує, як правило, стійкість і існує критичне запізнювання, при якому система виходить на межу стійкості - .

Частотний критерій стійкості А.В.Михайлова (1936 р.) заснований на аналізі характеристичного полінома системи, в який підставляється :

(4.26)

Вираз (4.26) можна подати у вигляді суми дійсної та уявної частини:

, (4.27)

де: - дійсна частина, складена з членів з парними степенями ;

- уявна частина, яка утримує члени з непарними степенями .

Кожному фіксованому значенню відповідає комплексне число, яке можна зобразити вектором на комплексній площині. При змінюванні від 0 до цей вектор описує криву, яка називається годограф Михайлова. За видом годографа можна оцінювати стійкість системи. При функція , що випливає з виразу (4.26), а при функція необмежено зростає, але проходить різну кількість квадрантів в залежності від порядка системи.

Критерій стійкості Михайлова формулюється так: автоматична система керування, якій відповідає рівняння (4.26), стійка, якщо при змінюванні від 0 до годограф огинає проти годинникової стрілки початок координат та проходить n квадрантів (n – порядок системи). Якщо система знаходиться на межі стійкості, то годограф проходить через початок координат (це відповідає наявності пари спряжених коренів).

ω=0

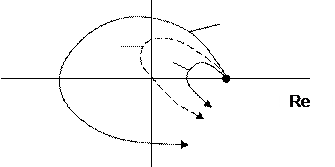
Рис.4.5. Годограф Михайлова

На рис.4.5 годограф 1 відповідає стійкій системі (n=4), 2 – на межі стійкості, 3 – нестійкій. При практичному використанні годографа Михайлова спочатку знаходять точки перетину його з координатними осями: при знаходять частоту, коли пересікається з уявною віссю і підставляють її значення у вираз для . Коли знайдено умови, за яких перетинає осі координат, тобто знайдено нулі і , то повністю годограф будувати не потрібно: стійкість має місце, якщо нулі та чергуються з ростом , починаючи з , тобто , а .

Якщо систему можна розбити на ланки, то годограф можна отримати за правилами перемноження векторів.

Для оцінки стійкості системи можна використовувати також логарифмічні частотні характеристики. Це засновано на висновках, які випливають з критерія стійкості Найквіста: система буде стійкою тоді, коли при досягненні фазовою частотною характеристикою значення

-180⁰ логарифмічна частотна характеристика буде від’ємною (криві 1, рис.4.6). Це значить, що АФХ розімкненої системи не охоплює точку

Рис.4.6. Логарифмічні частотні характеристики статичної системи

Date: 2016-02-19; view: 547; Нарушение авторских прав