Алгебраїчні критерії стійкості

Алгебраїчні критерії встановлюють необхідні та достатні умови стійкості на основі визначників, складених з коефіцієнтів характеристичного рівняння системи. Англійський математик Є.Раус (1877 р.) та швейцарський математик А.Гурвіц (1893 р.) в різній формі запропонували критерій, згідно якого умови стійкості зводяться до виконання нерівностей, які зв’язують коефіцієнти рівняння системи. Для розв’язання прикладних задач ці критерії об’єднують в один – Рауса-Гурвіца. В загальному випадку ці критерії призначались для розв’язання чисто математичної задачі – дослідження стійкості розв’язків лінійного диференціального рівняння. Вище було показано, що за допомогою такого рівняння описується поведінка лінійної АСР.

На основі характеристичного полінома:

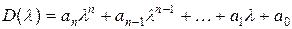(4.11)

складається визначник:

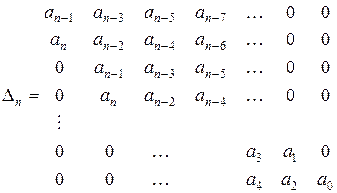(4.12)

Вираз (4.12) називається визначником Гурвиця і при його складанні виконуються правила:

- визначник має n рядків та n стовпців, в першому рядку розташовуються “непарні” коефіцієнти, після чого рядок доповнюється до числа n нулями;

- другий рядок включає всі “парні” коефіцієнти і також доповнюється нулями до числа n;

- третій та четвертий рядки отримують зсувом вправо відповідно першого та другого рядків на один елемент, а зліва проставляється нуль. Аналогічно отримують і наступні рядки;

- в головній діагоналі визначника розташовуються всі коефіцієнти, крім .

Критерій стійкості Рауса-Гурвиця формулюється так: автоматична система, яка описуються характеристичним поліномом (4.11) стійка, якщо при визначник та всі його діагональні мінори додатні. (Мінор – визначник, складений з елементів, розташованих на перетині будь-яких k рядків та k стовпців визначника). У виразі (4.12) мінори виділені пунктиром.

Останній стовпець визначника має лише один елемент , тому використовується відома залежність:

, (4.13)

яка розподається на дві за умови : . Коли , система знаходиться на межі стійкості. При цьому при існує один нульовий корінь (аперіодична межа стійкості), а при існує пара уявних коренів (коливальна межа стійкості).

Розглянемо використання алгебраїчного критерія для системи різних порядків. Для системи першого порядку характеристичний поліном має вигляд:

, (4.14)

а умова стійкості:

. (4.15)

Для системи другого порядку:

, (4.16)

, (4.17)

Таким чином, для системи першого і другого порядків необхідною і достатньою умовою стійкості є додатність всіх коефіцієнтів характеристичного рівняння.

Для системи третього порядку:

, (4.18)

(4.19)

Умови стійкості:

(4.20)

Остання нерівність за умови потребує . Таким чином, для системи 3-го порядку забезпечення стійкості вимагає не лише додатності всіх коефіцієнтів характеристичного рівняння, а й певного співвідношення між ними.

Для системи 4-го порядка:

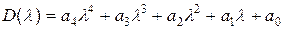(4.21)

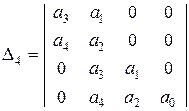(4.22)

Умова стійкості:

(4.23)

Для систем високих порядків () використання алгебраїчного критерія Рауса-Гурвиця стає незручним і потребує громіздких виразів. Крім того, цей критерій не дає можливості визначити, які заходи необхідно здійснити для забезпечення стійкості.

В теорії автоматичного керування використовується також алгебраїчний критерій Льєнара-Шіпара (1914 р.), який спрощує використання критерія Рауса-Гурвиця. Доведено, що необхідною і достатньою умовою стійкості при є вимога додатності всіх визначників з парними індексами або всіх визначників з непарними індексами .

Date: 2016-02-19; view: 519; Нарушение авторских прав