
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача 2.4. Расчет цепей со смешанным соединением приемников
|
|
Построение векторной диаграммы токов и топографической диаграммы напряжений
На рис. 2.10 изображена схема цепи с последовательно-параллельным соединением приемников. Значение действующего значения синусоидального напряжения  на зажимах цепи, активных
на зажимах цепи, активных  , индуктивных
, индуктивных  и емкостных
и емкостных 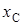 сопротивлений приведены в табл. 2.4.
сопротивлений приведены в табл. 2.4.
Требуется:
1) определить сопротивления ветвей  ,
,  ,
, 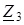 и всей цепи
и всей цепи  ;
;
2) найти токи ветвей 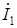 ,
, 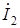 и всей цепи
и всей цепи  ;
;
3) составить баланс активных, реактивных и полных мощностей;
4) построить векторную диаграмму токов и потенциальную диаграмму напряжений.
Таблица 2.4
Исходные данные
| Варианты |  , В , В
| Сопротивления, Ом | Схема цепи | ||||||
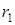
| 
| 
| 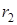
|  
| 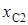
| 
| |||
| – | Рис. 2.10 (1) | ||||||||
| – | – | Рис. 2.10 (2) | |||||||
| – | Рис. 2.10 (3) | ||||||||
| – | – | Рис. 2.10 (4) | |||||||
| – | Рис. 2.10 (5) | ||||||||
| – | – | Рис. 2.10 (6) | |||||||
| – | – | – | Рис. 2.10 (7) | ||||||
| – | – | Рис. 2.10 (8) | |||||||
| – | Рис. 2.10 (9) | ||||||||
| – | Рис. 2.10 (0) |
Пример
Сопротивления участков цепи (рис. 2.11) равны: 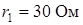 ;
; 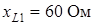 ;
;  ;
;  ;
; 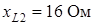 ;
; 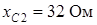 ;
; 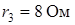 ;
;  . Действующее значение напряжения источника
. Действующее значение напряжения источника  .
.
Требуется:
1) определить сопротивления ветвей  ,
,  ,
, 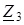 и всей цепи
и всей цепи  ;
;
2) рассчитать токи ветвей 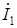 ,
, 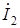 и всей цепи
и всей цепи  ;
;
3) определить комплексы напряжений на каждой ветви 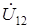 ,
,  ;
;
4) составить баланс активных, реактивных и полных мощностей;
5) построить векторную диаграмму токов и топографическую диаграмму напряжений.
Решение
1. Комплексные сопротивления ветвей
 ;
;
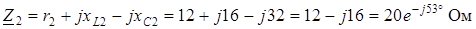 ;
;
 .
.
Эквивалентное сопротивление параллельных ветвей

Эквивалентное сопротивление цепи
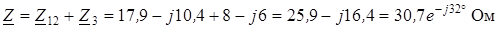 .
.
2. Ток всей цепи
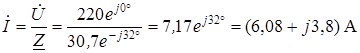 .
.
Напряжение на параллельно включенных ветвях
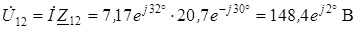 .
.
Напряжение на третьей ветви
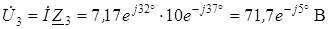 .
.
Токи в параллельных ветвях
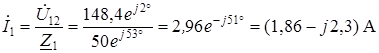 ;
;
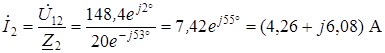 .
.
3. Мощности цепи
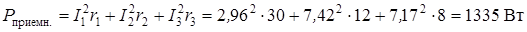 ;
;

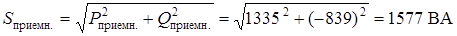 .
.
Полная мощность источника
 .
.
Так как 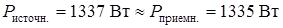 ;
;
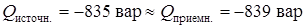 ;
;
 ,
,
следовательно, в данной цепи выполняется баланс активных, реактивных и полных мощностей источников и приемников энергии.
4. Векторная диаграмма токов и топографическая диаграмма напряжений цепи представлены на рис. 2.12.
В масштабе на комплексной плоскости отложены векторы токов 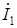 ,
, 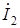 и
и  , их проще построить, пользуясь алгебраической формой записи, тогда и без транспортира построения будут точными. Проверяем равенство векторов
, их проще построить, пользуясь алгебраической формой записи, тогда и без транспортира построения будут точными. Проверяем равенство векторов  .
.
Для построения топографической диаграммы необходимо рассчитать действующие значения напряжений на отдельных элементах цепи:



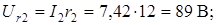
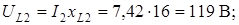
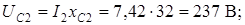

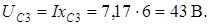
Примем потенциал точки  равным нулю (заземление одной точки электрической цепи не ведет к перераспределению токов). Эта точка на диаграмме совпадает с началом координат.
равным нулю (заземление одной точки электрической цепи не ведет к перераспределению токов). Эта точка на диаграмме совпадает с началом координат.
Перейдем от точки  электрической схемы к точке
электрической схемы к точке  , через емкость
, через емкость  протекает ток
протекает ток 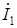 , который по фазе опережает вектор напряжения на емкости
, который по фазе опережает вектор напряжения на емкости  на
на  (за положительное направление вращения векторов принято направление против часовой стрелки). Отложим под углом
(за положительное направление вращения векторов принято направление против часовой стрелки). Отложим под углом  к вектору тока
к вектору тока 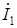 вектор
вектор  , его длина в масштабе равна
, его длина в масштабе равна 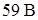 .
.
Через индуктивность 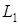 также протекает ток
также протекает ток 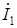 , который должен по фазе отставать от вектора напряжения
, который должен по фазе отставать от вектора напряжения  на
на  , следовательно, вектор
, следовательно, вектор  направим в сторону, противоположную вектору
направим в сторону, противоположную вектору  , его длина в масштабе равна
, его длина в масштабе равна  , получим точку
, получим точку  .
.
Перейдем от точки  электрической схемы к точке
электрической схемы к точке 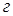 , падение напряжения на активном сопротивлении
, падение напряжения на активном сопротивлении 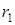
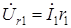 совпадает по направлению с током
совпадает по направлению с током 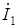 . Построив из точки
. Построив из точки  вектор
вектор 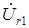 , параллельный вектору
, параллельный вектору 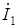 , получим на диаграмме точку
, получим на диаграмме точку 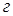 .
.
Теперь перейдем от точки  в точку
в точку 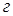 по второй ветви. Построение аналогично предыдущему, только векторы напряжений на элементах второй ветви связаны с направлением вектора тока
по второй ветви. Построение аналогично предыдущему, только векторы напряжений на элементах второй ветви связаны с направлением вектора тока 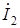 . Если все построения выполнены правильно, то конец вектора
. Если все построения выполнены правильно, то конец вектора 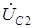 совпадет с точкой
совпадет с точкой 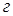 .
.
Через емкость  и активное сопротивление
и активное сопротивление  протекает ток
протекает ток  , который опережает по фазе вектор напряжения
, который опережает по фазе вектор напряжения 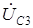 на
на  и совпадает по направлению с вектором напряжения
и совпадает по направлению с вектором напряжения 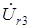 . Построив из точки г вектор
. Построив из точки г вектор 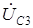 (угол между векторами
(угол между векторами  и
и 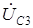 равен
равен  ), получим на диаграмме точку
), получим на диаграмме точку 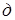 . Построив из точки
. Построив из точки 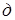 вектор
вектор 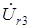 (вектор
(вектор 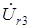 параллелен вектору
параллелен вектору  ), получим на диаграмме точку
), получим на диаграмме точку 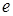 .
.
Вектор, соединяющий точку  с точкой
с точкой 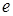 и направленный из точки
и направленный из точки  к точке
к точке 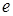 , изображает напряжение
, изображает напряжение  на зажимах цепи. Геометрическая сумма векторов напряжений на отдельных участках схемы
на зажимах цепи. Геометрическая сумма векторов напряжений на отдельных участках схемы 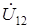 и
и  в сумме равна приложенному напряжению
в сумме равна приложенному напряжению  , начальную фазу которого в начале задачи приняли нулевой (
, начальную фазу которого в начале задачи приняли нулевой (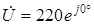 ).
).
Date: 2016-02-19; view: 655; Нарушение авторских прав