Задача 2.2. Комплексный метод расчета цепей с синусоидальной ЭДС

Топографическая диаграмма цепи

В неразветвленной электрической цепи (рис. 2.4) заданы сопротивления участков и действующее значение синусоидального напряжения источника (табл. 2.2)

Требуется:

1) определить комплексные значения сопротивления цепи , тока и мощности ;

2) найти напряжения на всех элементах цепи;

3) построить топографическую диаграмму цепи.

Таблица 2.2

Исходные данные

Варианты	, В	Сопротивления, Ом	Схема цепи
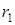
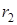
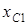
							–	Рис. 2.4 (1)
					–			Рис. 2.4 (2)
					–		–	Рис. 2.4 (3)
					–		–	Рис. 2.4 (4)
					–		–	Рис. 2.4 (5)
							–	Рис. 2.4 (6)
					–			Рис. 2.4 (7)
							–	Рис. 2.4 (8)
					–		–	Рис. 2.4 (9)
							–	Рис. 2.4 (0)

Пример

Сопротивления участков неразветвленной электрической цепи (рис. 2.5) равны: , , , , , . Действующее значение синусоидального напряжения на зажимах цепи .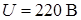

Требуется:

1) определить комплексные значения тока и мощности ;

2) найти комплексные напряжения на всех элементах цепи;

3) построить топографическую диаграмму цепи.

Решение

1. Комплексное сопротивление цепи

где .

Начальную фазу напряжения примем равной нулю, тогда 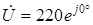и ток в цепи

.

Комплекс полной мощности цепи равен произведению комплекса напряжения на сопряженный (изменяется знак у мнимой части) комплекс тока

.

Следовательно, активная мощность цепи , реактивная и полная мощность .

2. Напряжения на элементах цепи равны:

;

;

.

3. Строим векторную диаграмму тока и топографическую диаграмму напряжений (рис. 2.6). Для этого примем потенциал точки 1 равным нулю, т.е. . Обходя контур в направлении, встречном положительному направлению тока, определим потенциалы остальных точек цепи. Потенциал точки 2 выше потенциала точки 1 на величину падения напряжения в сопротивлении , т.е.:

.

Потенциал точки 3 выше потенциала точки 2 на величину падения напряжения на индуктивном сопротивлении , т.е.:

.

Аналогично находят комплексные потенциалы остальных точек цепи:

;

;

;

.

Таким образом, для определения комплексных потенциалов цепи необходимо складывать векторы соответствующих напряжений на элементах контура. Построения начинаем с вектора тока. Далее отложим на комплексной плоскости потенциалы точек цепи. Отрезок, соединяющий любые две точки топографической диаграммы, определяет комплексное напряжение между этими точками цепи.

Date: 2016-02-19; view: 686; Нарушение авторских прав