Управляемость и наблюдаемость

Если линейная система имеет различные характеристические числа λ_i и описывается уравнениями состояния в нормальной форме:

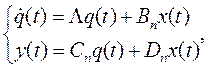
то каждая из переменных состояния q_i характеризует различные частоты (моды) системы. Для этой формы условия управляемости и наблюдаемости вполне очевидны.

Управляемость является функцией связи между входами и различными собственными частотами системы. Отдельная частота (или переменная состояния) системы неуправляема, если вход не оказывает воздействия на эту частоту. Это соответствует наличию нулевой строки в матрице В_n.

Таким образом, можно сформулировать критерий полной управляемости линейной системы с разными λ_i, описываемой уравнениями состояния внормальной форме:

Для того чтобы система была полностью управляема, в матрице управления В_n не должно быть нулевой строки.

Пример 1. Используем принцип доказательства «от противного» и рассмотрим систему из примера, в которой нарушено условие полной управляемости. Действительно, если допустить, что в матрице В_n имеется нулевая строка (например, вторая), то получим:

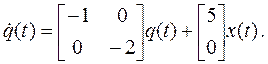
Если перейти от векторно-матричной формы записи уравнения состояния к обычной системе двух дифференциальных уравнений, то получим:

Во второе уравнение не попадает входной (управляющий) сигнал x(t). Это и означает, что состоянием системы q₂ невозможно управлять, на него невозможно воздействовать входным сигналом (тогда как состоянием q₁ управлять с помощью входа можно). Таким образом, рассмотренная в данном примере система – не полностью управляемая, причем об этом свидетельствует именно нулевая вторая строка в матрице управления В_n. Если бы в матрице В_n нулевой оказалась первая строка, то невозможно было бы управлять состоянием q₁.

Пример 2. Примером реальной не полностью управляемой системы может служить автомобиль, из тормозной системы которого вытекла тормозная жидкость. Нажатие на педаль тормоза (входной управляющий сигнал x₁)не будет влиять на модуль скорости (состояние q₁). С другой стороны, такая неисправная система не является полностью неуправляемой, так как направлением вектора скорости, связанным с угловым положением передних колес (состояние q₂), управлять можно с помощью другого входного управляющего воздействия – угла поворота рулевого колеса (x₂).

Из данного примера очевиден вывод об опасности потери управляемости. Крайне опасно также отсутствие управляемости с самого начала, например, при проектировании системы или при исследовании неизвестной системы, например, вирусной инфекции. Управляемость– свойство структуры системы.

С другой стороны, наблюдаемость также является свойством структуры системы.

Наблюдаемость является функцией связи между различными собственными частотами системы и ее выходами. Отдельная частота (переменная состояния) не наблюдаема ни на одном их выходов системы, если не существует связи между этой частотой и произвольным выходом системы. Это соответствует наличию нулевого столбца в матрице C_n.

Таким образом, можно сформулировать критерий полной наблюдаемости линейной системы с разными λ_i, описываемой уравнениями состояния в нормальной форме:

Для того чтобы система была полностью наблюдаема, в матрице наблюдения C_n не должно быть нулевого столбца.

Покажем на примере, к чему приводит нарушение условия полной наблюдаемости.

Пример 3. Возьмем уравнение наблюдения из ранее рассмотренного примера:

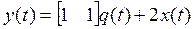
и сделаем нулевым первый столбец в матрице наблюдения C_n:

Раскрытие этого векторно-матричного уравнения приведет к скалярному уравнению наблюдения (поскольку выход y только один):

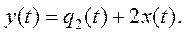
Как видно из уравнения, переменная состояния q₁(t) не наблюдается – она не попадает в выходной сигнал y(t). Если бы в матрице наблюдения C_n нулевым был второй столбец, то не наблюдаемым было бы состояние q₂.

Пример 4. Примером реальной не полностью наблюдаемой системы может служить тот же автомобиль, на приборную панель которого не поступает сигнал от датчика температуры охлаждающей жидкости (причина может быть любая: неисправность самого датчика, разрыв провода или просто отсоединенный разъем). Система при этом работает, в принципе можно ехать, но в случае превышения температурного предела (около 95^о С) водитель этого не увидит и не среагирует, что может привести к перегреву двигателя и серьезному ремонту. Именно для наблюдения за наиболее важными переменными состояния на панели управления сложных систем выводятся показания соответствующих датчиков. Потеря наблюдаемости, даже частичная, чрезвычайно опасна и может привести к катастрофическим последствиям.

Управляемостьи наблюдаемость– структурные свойства системы, поэтому повлиять на них с помощью изменения одних только параметров невозможно. Нужно внести соответствующие изменения в структуру системы.

Оценка управляемости позволяет понять, какими переменными состояния системы мы можем управлять, а какими нет. Чаще всего структурная невозможность управления каким-либо состоянием приводит к необходимости отказа от такой структуры или вообще от такой системы и замены их другими.

Оценка наблюдаемости позволяет понять, какие переменные состояния системы мы можем наблюдать (видеть, измерять), чтобы не допустить, например, возрастания значений этих переменных состояния сверх предельно допустимых значений. Например, нетрудно представить, как важно наблюдать за давлением в паровом котле, концентрацией окиси углерода в закрытом помещении, температурой в холодильной камере, скоростью оборотов турбины ГЭС или температурой реактора атомной подводной лодки.

Можно выделить четыре подсистемы, проявляющие свойства управляемости, наблюдаемости, неуправляемости и ненаблюдаемости (рис. 2.14).

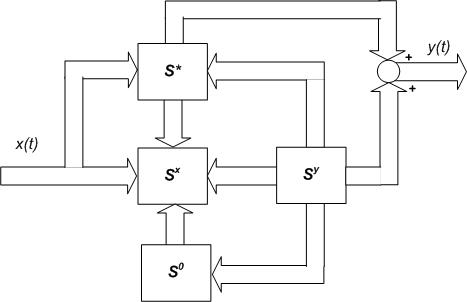
Рис. 2.14. Подсистемы: S* – управляемая и наблюдаемая; S^x –управляемая, но ненаблюдаемая; S^y – наблюдаемая, но неуправляемая; S⁰ – неуправляемая и ненаблюдаемая

Требование управляемости и наблюдаемости всей системы состоит в том, чтобы система содержала только подсистему S*. Однако, например, при проектировании, если не учесть остальные подсистемы S^x, S^y, S⁰, то можно прийти к выводу о нормальной работоспособности S*,в то время как в действительности система в целом не работоспособна. Так, если подсистема S⁰ содержит неустойчивые частоты, то возбуждение этих частот при нулевых начальных условиях приведет к неустойчивости выхода. То же касается и подсистем S^x и S^y.

Вопросы к разделу 2.7

1. В чем заключается критерий полной управляемости линейных динамических систем?
2. Почему при определении полной управляемости исследуются именно строки матрицы объекта?
3. К чему может привести неполная управляемость системы?
4. Что означает случай полной неуправляемости?
5. В чем заключается критерий полной наблюдаемости линейных динамических систем?
6. Почему при определении полной наблюдаемости исследуются именно столбцы матрицы наблюдения?
7. К чему может привести неполная наблюдаемость системы?
8. Что означает случай полной ненаблюдаемости?
9. Приведите примеры неуправляемости и ненаблюдаемости систем.

Date: 2016-02-19; view: 591; Нарушение авторских прав