
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические сведения. Особый класс систем ортогональных функций составляют системы кусочно-постоянных функций, таких как функции Уолша
|
|
Особый класс систем ортогональных функций составляют системы кусочно-постоянных функций, таких как функции Уолша, Адамара и Хаара. Эти системы имеют большое практическое значение, особенно для цифровых систем, поскольку они характеризуются высокоэффективными алгоритмами быстрых преобразований.
В 1923 году американский ученый Уолш получил полную систему ортонормированных функций, которая дополняет систему функций Радемахера. Множество функций Уолша обычно разделяется на три группы, отличающиеся порядком расположения в системе.
Общеприняты следующие упорядочения (способы определения функций Уолша):
· упорядочение по частоте (по Уолшу с помощью функций Радемахера);
· упорядочение по Пэли (диадическое);
· упорядочение по Адамару, где под частотой функции понимается число пересечений нулевого уровня в единицу времени.
Рассмотрим способ, основанный на взаимосвязи функций Уолша с функциями Радемахера и способ, основанный на матрицах Адамара.
Функции Радемахера получаются из синусоидальных функций с помощью соотношения

 , (3.1)
, (3.1)
где аргумент t – безразмерное время, т.е. время, нормированное к произвольному интервалу  , а целое положительное число k – порядок функции. Символом sign (сигнум-функция) обозначается функция:
, а целое положительное число k – порядок функции. Символом sign (сигнум-функция) обозначается функция:
 (3.2)
(3.2)
Функции Радемахера принимают одно из двух значений 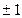 и имеют вид меандра.
и имеют вид меандра.
Функции Радемахера ортонормированны с единичной весовой функцией на интервале  , т.к. для любых двух функций
, т.к. для любых двух функций  ,
,  имеют место соотношения:
имеют место соотношения:
 (3.3)
(3.3)
Все функции Радемахера являются нечетным и относительно середины интервала определения и не могут быть использованы для аппроксимации сигналов, четных относительно этой точки. Иными словами, система функций Радемахера – неполная. На рис. 3.1 приведены функции Радемахера для 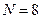 .
.
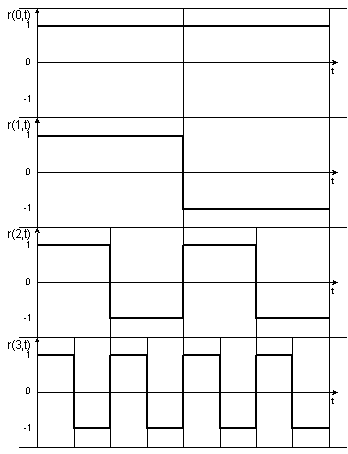
Рис. 3.1 Функции Радемахера для N=8
Обозначив для краткости r(m,t)=rm(t), для N=8 будем иметь:
Если  = ++++----
= ++++----
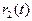 = ++--++--
= ++--++--
 = +-+-+-+-,
= +-+-+-+-,
где “+” соответствует +1, а “–” соответствует –1.
Функции Уолша, образующие полную ортонормированную систему, можно сформировать, образуя произведения соответствующих функций Радемахера. Первые восемь функций Уолша представлены на рис. 3.2.

Рис. 3.2. Первые восемь функций Уолша
В свою очередь функции Уолша можно представить следующим образом:
wal(0,t)= ++++++++
wal(1,t)=r1= ++++----
wal(2,t)=r1r2= ++----++
wal(3,t)=r2= ++--++--
wal(4,t)=r2r3= +--++--+
wal(5,t)=r1r2r3= +--+-++-
wal(6,t)=r1r3= +-+--+-+
wal(7,t)=r3= +-+-+-+-
Сопоставление этих функций с функциями Радемахера позволяет составить очевидные соотношения, согласно которым каждая функция Уолша wal(n,t) с номером n, входящая в систему из  функций, является произведением степеней первых n функций Радемахера.
функций, является произведением степеней первых n функций Радемахера.
Принцип нахождения показателей этих степеней определяется двоичным представлением номера функции n. Примем следующие обозначения для разрядов, составляющих двоичное представление числа n:  - первый разряд,
- первый разряд,  - второй разряд, и так далее до
- второй разряд, и так далее до 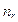 , то есть r-го разряда двоичного представления натурального числа n. При такой нумерации
, то есть r-го разряда двоичного представления натурального числа n. При такой нумерации  оказывается старшим разрядом числа n, а
оказывается старшим разрядом числа n, а 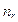 - младшим.
- младшим. 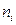 может принимать одно из двух значений – нуль или единица. Будем считать, что
может принимать одно из двух значений – нуль или единица. Будем считать, что 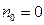 по определению. Используя символ
по определению. Используя символ 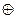 для обозначения операции поразрядного сложения по модулю 2, способ построения функций Уолша можно выразить аналитически для любого
для обозначения операции поразрядного сложения по модулю 2, способ построения функций Уолша можно выразить аналитически для любого  в виде следующего соотношения:
в виде следующего соотношения:
 (3.4)
(3.4)
Поясним применение данной формулы на примере шестой функции Уолша (n=6), входящей в систему размером  . Произведение состоит из трех множителей вида:
. Произведение состоит из трех множителей вида:
при k=1  ,
,
при k=2  ,
,
при k=3  .
.
На основе двоичного представления числа n=6 не сложно установить, что 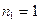 ,
,  ,
, 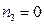 .
.
Таким образом,  ,
,  ,
,  и по формуле:
и по формуле:
 .
.
Функции Радемахера перемножаются при использовании кода Грея. В некоторых практических приложениях, например в аналого-цифровых преобразованиях, желательно использовать коды, у которых все следующие друг за другом кодовые слова различаются только одной цифрой в некотором разряде. Коды, обладающие таким свойством, называются циклическими.
Очень важным циклическим кодом является код Грея. Двоичное представление числа может быть легко преобразовано в код Грея с помощью полусумматоров.
Пусть gn-1gn-2…g2g1g0 – кодовое слово в n -разрядном двоичном коде Грея, соответствующее двоичному числу bn-1bn-2…b2b1b0. Тогда gi может быть получена как
gi=bi Å bi+1, 0 £ i £ n-2;
gn-1=bn-1,
где Å означает сложение по модулю два, которое определяется как
0 Å 0=0
1 Å 0=1
0 Å 1=1
1 Å 1=0
Например, код Грея, соответствующий двоичному числу 101101, может быть образован как на рис. 3.3. Трехразрядный код Грэя показан в табл. 3.1.

Рис. 3.3. Преобразование двоичного кода в код Грея
Таблица 3.1
Трехразрядный код Грэя
| Десятичное число | Код Грея | Двоичный код | ||||
| g2 | g1 | g0 | b2 | b1 | b0 | |
Преобразование кода Грея в двоичный код начинается с цифры самого левого разряда и движения вправо, принимая bi=gi, если число единиц, предшествующих gi, четно и  (черта обозначает инвертирование), если число единиц, предшествующих gi, нечетно. При этом нулевое число единиц считается четным. Пример двоичного числа, соответствующее коду Грея 1001011, показан на рис. 3.4.
(черта обозначает инвертирование), если число единиц, предшествующих gi, нечетно. При этом нулевое число единиц считается четным. Пример двоичного числа, соответствующее коду Грея 1001011, показан на рис. 3.4.

Рис. 3.4. Преобразование кода Грея в двоичный код
Приведем некоторые свойства функций Уолша.
1. Функции Уолша ортонормированны на интервале  :
:

2. Функции Уолша обладают свойством мультипликативности, т.е. перемножение двух функций Уолша дает другую функцию Уолша, причем верно соотношение:
 .
.
3. Функции Уолша обладают свойством симметрии, проявляющимся в том, что все выводы относительно i справедливы также и относительно t. Например, свойство мультипликативности с учетом свойства симметрии запишется в виде
 .
.
4. Умножение любой функции самой на себя дает функцию нулевого порядка  , так как в результате получаются только произведения вида (+1)(+1) и (-1)(-1). Таким образом,
, так как в результате получаются только произведения вида (+1)(+1) и (-1)(-1). Таким образом,
 .
.
5. Очевидно также, что умножение  на
на  не изменяет функцию
не изменяет функцию  .
.
Способ нумерации функций в системе называется упорядочением. Функции Уолша, сформированные в соответствии с выражением (3.4), упорядочены по Уолшу.
В ряде практических задач целесообразно пользоваться иными способами упорядочения. Часто применяются функции Уолша, упорядоченные по Адамару [had(h,t)] и по Пэли [pal(p,t)].
Независимо от упорядочения функции Уолша, составляющие систему из  функций, всегда можно представить в виде произведения степеней первых r функций Радемахера. Принцип же нахождения показателей этих степеней индивидуален для каждого упорядочения.
функций, всегда можно представить в виде произведения степеней первых r функций Радемахера. Принцип же нахождения показателей этих степеней индивидуален для каждого упорядочения.
Остановимся на упорядочении по Адамару. При N=2n матрица Адамара может быть получена с помощью соотношения
 ;
;
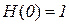 .
.
Матрица Адамара также может быть получена из ядра  c помощью кронекеровского произведения, т.е.
c помощью кронекеровского произведения, т.е.
 .
.
Далее (табл. 3.2, 3.3) приводятся нумерация функций Уолша в базисе из 16 функций при различных способах упорядочения и нумерация для базиса из 8 функций. Сравнение таблиц показывает, что нумерация одних и тех же функций в упорядочении Адамара меняется в зависимости от размерности базиса.
| Таблица 3.2 Нумерация функций Уолша при различных способах упорядочения, N=16 | Таблица 3.3 Нумерация функций Уолша при различных способах упорядочения, N=8 | |||||
| wal(n,t) | had(h,t) | pal(p,t) | wal(n,t) | had(h,t) | pal(p,t) | |
Быстрое преобразование Уолша можно получить с помощью технологии разбиения матриц. Графическая схема алгоритма показана на рис. 3.5. Рассмотрим вывод алгоритма для N=8. При N=8 в матричном виде преобразование Уолша можно записать как
 .
.
Используя соотношение  , H(3) можно выразить через H(2), что приводит к
, H(3) можно выразить через H(2), что приводит к
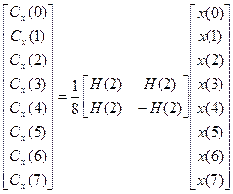 .
.
Из разбиения матрицы следует, что
 и
и  ,
,
где  ;
;
 .
.
Подставляя вместо  , будем иметь
, будем иметь
 и
и
 .
.
Тогда получим
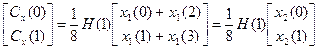 ;
;
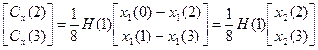 ;
;
 ;
;
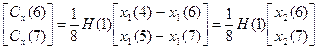 .
.
Так как  , то окончательно получим
, то окончательно получим
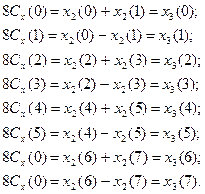
Для N=2n:
1. Общее число итераций равно n=log2N. Индекс r принимает значения r=1,2,..., n.
2. В r итерации участвует 2r-1 групп по N/2r-1 элементов. Половина элементов в каждой группе связана с операцией сложения, а другая половина – с операцией вычитания.
3. Общее число арифметических операций, необходимое для вычисления всех коэффициентов преобразования, равняется приблизительно Nlog2N.
На рис. 3.5 приведена граф-схема процедуры быстрого алгоритма Уолша.
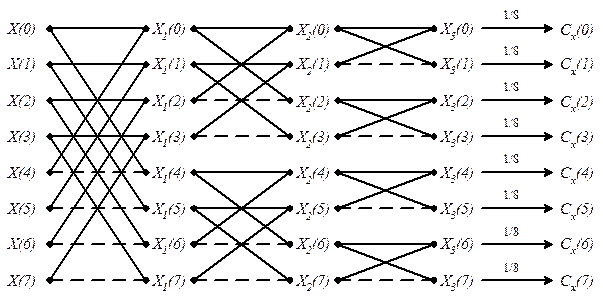
Рис. 3.5. Процедура быстрого алгоритма Уолша
Date: 2016-02-19; view: 1029; Нарушение авторских прав