
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Быстрое преобразование Фурье (БПФ)
|
|
Быстрое преобразование Фурье (FFT) является не более, чем алгоритмом для ускоренного вычисления ДПФ путем сокращения требуемого числа операций умножения и сложения. Данное преобразование было предложено в 1960-ых годах. Алгоритм быстрого преобразования Фурье значительно сокращает количество арифметических операций и объем памяти, необходимой для вычисления ДПФ. ДПФ может быть сильно упрощено, если использовать свойства симметрии и периодичности коэффициентов поворота.
При вычислении N-точечного ДПФ требуется  вычислений с комплексными числами, а при реализации N-точечного БПФ
вычислений с комплексными числами, а при реализации N-точечного БПФ  вычислений с комплексными числами. Вычислительная эффективность БПФ по сравнению с ДПФ становится весьма существенной, когда количество точек БПФ увеличивается до нескольких тысяч (табл. 1.1).
вычислений с комплексными числами. Вычислительная эффективность БПФ по сравнению с ДПФ становится весьма существенной, когда количество точек БПФ увеличивается до нескольких тысяч (табл. 1.1).
Таблица 1.1
Эффективность БПФ
| N | Умножений при ДПФ | Умножений при БПФ | Эффективность БПФ |
| 65 536 | 1 024 | 64: 1 | |
| 262 144 | 2 304 | 114: 1 | |
| 1 024 | 1 048 576 | 5 120 | 205: 1 |
| 2 048 | 4 194 304 | 11 264 | 372: 1 |
| 4 096 | 16 777 216 | 24 576 | 683: 1 |
Если необходимо рассчитать только несколько точек спектра, ДПФ может быть более эффективным. Вычисление одного выходного отсчета спектра с использованием ДПФ требует только N умножений с комплексными числами.
Мы будем предполагать далее, что N=2n. При этом общность не теряется, так как N выбирается достаточно большим для того, чтобы удовлетворять теореме дискретизации Котельникова, т.е.
N ³ 2BT,
где B – полоса частот сигнала x(t); T – его длительность.
Теорема Котельникова-Найквиста-Шеннона: если сигнал таков, что его спектр ограничен частотой F, по после дискретизации сигнала с частотой не менее 2F можно восстановить непрерывный сигнал по полученному цифровому сигналу абсолютно точно. Для этого нужно проинтерполировать цифровой сигнал «между отсчетами» специального вида функциями.
Рассмотрим случай вещественно-значной последовательности {X(m)} при N=8. Из свойства комплексной сопряженности ДПФ следует, что
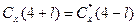 ;
;  .
.
Тогда
 ;
; 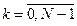 ;
;
W=e-i2p/8=e-ip/4;
 . (1.17)
. (1.17)
Используя свойство N-периодичности экспонент, для N=8 матрица будет иметь вид


 .
.
Из свойства симметрии экспоненциальных функций следует, что
Wk+N/2=-Wk, где  .
.
То есть W4=-W0;
W5=-W1;
W6=-W2;
W7=-W3.
Тогда матрица F будет иметь вид


 .
.
Используя двоичную инверсию (перестановку) строк,
(0,1,2,3,4,5,6,7)® (0,4,2,6,1,5,3,7) будем иметь


 =
=
=  . (1.18)
. (1.18)
В свою очередь, матрицы A11 и B11 можно представить в виде, где верхний индекс представляет собой номер шага процедуры БПФ
 (1.19)
(1.19)
Подставляя выражения для A11 и B11 в (1.18) получим
 ;
;
 ;
;
 ;
;
 . (1.20)
. (1.20)
Наконец, на последнем шаге получим
 (1.21)
(1.21)
Описанный алгоритм удобно представить графически (рис. 1.6).

Рис. 1.6. Граф-схема быстрой процедуры вычисления коэффициентов преобразования Фурье
Для определения степеней W на одном шаге необходимо выразить последовательность l=0, 1, 2, …, N/2-1 в виде (n-1) – разрядных двоичных последовательностей. В результате для N=16, к примеру, получим множество
S1=(000,001,010,011,100,101,110,111).
Для получения S2 необходимо выполнить двоичную инверсию каждой (n-1) -разрядной последовательности множества S1, т.е.
S2=(000,100,010,110,001,101,011,111),
и записать двоичную последовательность в виде десятичных чисел
S3=(0,4,2,6,1,5,3,7),
и таким образом имеем W0, W4, W2, W6, W1, W5, W3, W7. (табл. 1.2).
Итерация r для БПФ состоит из 2r-1 групп, где  (N=2n). Для N=16,
(N=2n). Для N=16,  .
.
Таблица 1.2
Значения степени W
| Номер итерации | Степени W (N=16) |
| W0 W0 W0 W0 W0 W0 W0 W0 W0 W0 W0 W0 W0 W0 W0 W0 | |
| W0 W0 W0 W0 W0 W0 W0 W0 W4 W4 W4 W4 W4 W4 W4 W4 | |
| W0 W0 W0 W0 W4 W4 W4 W4 W2 W2 W2 W2 W6 W6 W6 W6 | |
| W0 W0 W4 W4 W2 W2 W6 W6 W1 W1 W5 W5 W3 W3 W7 W7 |
Первый элемент первой строки таблицы равен нулю. Последующие первые элементы каждой из строк определяются как ns=N/2s, где  , N=2n. Каждая k строка таблицы получается прибавлением элемента nk-1 к каждому элементу предыдущих строк. Тогда таблица будет иметь вид
, N=2n. Каждая k строка таблицы получается прибавлением элемента nk-1 к каждому элементу предыдущих строк. Тогда таблица будет иметь вид
0
n1
n2 (n1+n2)
n3 (n1+n3) (n2+n3) (n1+n2+n3)
n4 (n1+n4) (n2+n4) (n1+n2+n4) …
.
.
nk …
Требуемая последовательность Ln, соответствующая двоичной инверсии, определяется как Ln=(0, n1, n2, (n1+n2), n3, (n1+n3), …, nk, …). В качестве примера рассмотрим случай для N=16. Тогда n1=8, n2=4, n3=2, n4=1, т.е. таблица будет иметь вид
0
8
4 12
2 10 6 14
1 9 5 13 3 11 7 15
Ln=(0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15).
Для обработки исходных данных (которые предполагаются комплексными) с помощью алгоритма БПФ требуется 2N ячеек оперативной памяти. Поэтому выходной массив может храниться в тех же ячейках памяти, что и исходный массив. Процедура перестановки данных может потребовать дополнительно 2N ячеек памяти. Таким образом, для алгоритма БПФ необходимо примерно 4N ячеек. В противоположность этому прямой метод требует приблизительно 2N2 ячеек памяти, т.к. необходимо запомнить N2 значений степеней W.
В общем виде матрицу преобразования Фурье в факторизованной форме можно представить как
 . (1.22)
. (1.22)
Для N=8 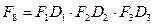 , где
, где  ; I4 – единичная матрица размерностью 4 ´ 4; D1 – диагональная матрица с элементами W0;
; I4 – единичная матрица размерностью 4 ´ 4; D1 – диагональная матрица с элементами W0;
 .
.
D2 -диагональная матрица с элементами W0, W2:
 ;
;
 ;
;  .
.
Факторизованная форма – это такая форма, когда в каждой строке матрицы, являющейся множителем, присутствует не более 2 значащих элементов, а остальные равны нулю.
Из вышесказанного следует сделать вывод о том, что при реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления последовательности отсчетов на части (прореживание по времени либо по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге (основание БПФ).
Date: 2016-02-19; view: 643; Нарушение авторских прав