Алгоритм БПФ (FFT) с прореживанием по времени (decimation-in-time, DIT)

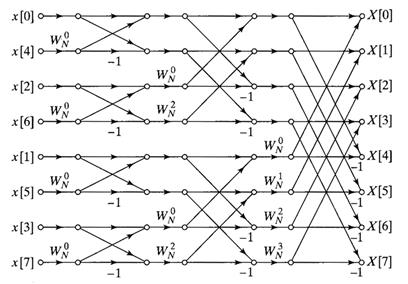
Рис. 1.7. Граф-схема алгоритма БПФ с прореживанием по времени

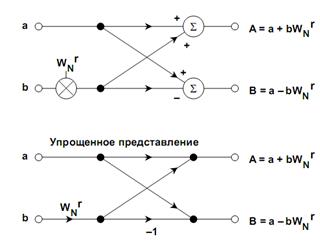
Рис. 1.8. Операция «бабочка» в алгоритме БПФ с прореживанием по времени

Алгоритм быстрого преобразования Фурье с прореживанием по времени можно выразить следующим образом.

АЛГОРИТМ БПФ(a, N, dir)

{

1. Если длина вектора равна 1, вернуть a.

2. Разбить вектор a на четную часть a^чет = (a₀,a₂,…,a_N-2)

и нечетную a^нечет = (a₁,a₃,…,a_N-1).

3. Рекурсивно вызвать БПФ на каждой из частей

b^чет = БПФ(a^{че т})

b^нечет = БПФ(a^нечет)

4. Объединение результатов.

a. (инициализация) Присвоить 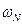значение главного комплексного корня N-й степени из единицы

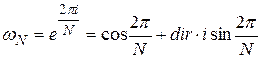
b. (инициализация) Присвоить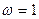

c. В цикле вычислить левую и правую часть одновременно:

for(j=0; j < N/2; j++)

{

}

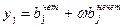
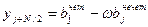
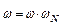
5. Вернуть вектор y.

}

При реализации алгоритма БПФ с прореживанием по времени происходит разбиение вектора на две части – четную и нечетную, после чего выполняется операция бабочка.

Ниже изображено дерево рекурсий, рис. 1.9. Каждый уровень, начиная снизу, соответствует проходу алгоритма по всему вектору и объединению сначала одиночных элементов в пары, затем пар в четверки и так далее до конца. Обратите внимание на то, что порядок индексов на верхнем уровне не соответствует нижнему. Это естественно, если учесть, что нечетные индексы после бабочки идут в правую половину вектора, а четные – в левую.

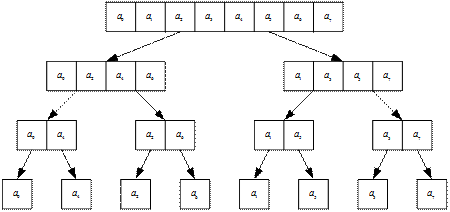
Рис. 1.9. Дерево рекурсий для 8 элементов

Date: 2016-02-19; view: 766; Нарушение авторских прав