Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
N А n А n А n А n A
|
|
1 2 3 4 5 6 7 8 9 10
36 33 32 34 31 33 28 29 32 36 31 33 28 30 36
45 42 39 46 38 41 39 44 46 41 40 40 46 39 38
1 56 49 49 2 48 51 53 3 49 54 54 4 49 49 54 5 56 49 48
30 34 36 32 35 36 31 31 36 35 28 36 36 31 34
44 38 38 39 38 42 46 40 43 40 43 39 41 38 40
6 49 53 50 7 48 50 55 8 54 55 49 9 54 50 50 10 51 55 55
36 33 33 32 29 29 29 33 31 32 32 35 30 29 29
42 38 45 44 41 45 40 46 40 42 44 41 39 43 46
11 52 56 55 12 48 48 56 13 51 50 49 14 55 53 54 15 49 56 50
28 32 36 31 28 30 28 34 35 29 31 31 34 36 36
40 40 45 44 46 40 45 40 39 46 39 43 39 45 38
16 50 55 49 17 53 56 48 18 48 53 48 19 56 48 53 20 49 52 48
31 36 30 32 29 29 29 35 30 29 33 35 36 35 31
40 45 40 44 41 45 41 44 41 39 41 44 38 41 39
21 51 55 48 22 48 48 56 23 48 49 48 24 56 53 56 25 55 55 53
31 35 33 35 30 30 33 32 28 35 29 36 29 32 36
38 39 42 44 42 41 41 41 44 38 45 42 40 46 42
26 53 52 51 27 48 54 49 28 56 54 49 29 51 49 54 30 49 52 53
36 29 28 33 32 32 35 29 32 30 29 32 36 34 29
41 44 40 45 45 41 41 39 41 38 44 41 40 43 38
31 55 51 51 32 55 51 54 33 51 51 53 34 48 48 55 35 52 55 52
Продолжение табл. 2.1
1 2 3 4 5 6 7 8 9 10
36 32 31 35 29 30 32 35 32 29 36 28 29 28 33
44 40 39 44 43 39 42 38 42 38 39 39 42 44 42
36 49 54 54 37 48 51 49 38 56 49 55 39 51 51 55 40 53 53 51
29 31 30 36 34 33 31 28 28 33 32 31 35 34 29
45 40 38 41 41 38 40 42 43 45 42 45 43 38 46
41 53 49 50 42 55 54 48 43 54 48 51 44 50 48 55 45 55 50 52
30 36 28 28 34 34 28 36 28 36 28 34 28 32 36
41 44 46 42 38 42 41 42 42 39 43 40 45 46 42
46 50 48 54 47 56 49 48 48 51 52 49 49 48 51 50 50 48 55 50
35 32 32 33 30 32 35 28 29 28 35 35 31 31 34
42 39 41 41 42 39 40 45 39 42 45 44 44 43 39
51 52 52 52 52 55 55 54 53 52 53 50 54 52 49 56 55 52 51 55
32 36 29 33 34 28 29 30 36 31 28 33 35 29 31
40 38 41 44 44 46 40 45 38 38 42 41 45 38 43
56 54 56 54 57 51 51 52 58 50 53 56 59 52 54 49 60 50 53 55
28 33 29 32 32 30 30 29 34 29 30 33 29 30 31
45 45 40 40 42 46 40 46 38 40 39 42 46 40 41
61 56 49 56 62 50 52 53 63 51 53 51 64 56 56 48 65 53 55 56
35 32 30 33 35 29 32 29 31 32 35 31 29 31 29
43 41 41 44 45 44 43 40 39 40 46 40 42 38 46
66 52 54 48 67 55 50 48 68 48 55 55 69 52 53 53 70 54 54 50
32 33 31 29 36 32 30 28 33 32 31 31 32 28 29
39 42 39 40 46 40 42 42 46 45 46 46 46 38 38
71 55 56 55 72 55 49 53 73 53 56 49 74 55 56 52 75 50 49 50
33 29 36 29 33 35 34 28 30 36 33 34 32 28 35
44 40 41 43 46 46 41 38 41 44 42 42 42 44 46
76 55 48 53 77 48 52 49 78 55 51 52 79 53 53 50 80 51 54 52
29 30 33 36 36 35 28 29 36 28 29 28 30 29 31
42 46 39 44 43 41 44 44 40 38 40 45 42 38 42
81 53 49 51 82 49 53 49 83 54 49 49 84 52 56 52 85 52 53 52
32 33 35 30 31 35 32 32 31 35 35 30 33 29 29
45 40 46 44 42 44 43 38 42 43 43 39 43 39 39
86 53 49 56 87 56 52 49 88 48 48 55 89 49 50 50 90 51 52 50
34 32 36 35 32 34 31 34 32 29 28 28 31 28 35
38 42 41 43 44 41 44 42 46 42 38 38 38 42 46
91 53 56 56 92 48 48 48 93 53 53 48 94 49 56 51 95 50 54 48
35 35 29 32 31 30 32 34 30 35 32 29 34 33 31
39 39 43 42 41 41 45 41 40 40 45 40 45 44 41
96 56 55 50 97 48 49 49 98 48 48 53 99 54 56 54 00 48 48 53
Задание 2.5
Найти обратную матрицу для той же матрицы А, что в зада-
нии 2.2.
При решении воспользоваться формулой, выражающей А-1
через алгебраические дополнения и определитель матрицы А.
Значение определителя взять из решения задания 2.2.
Задание 2.6
Пользуясь программным обеспечением ЭВМ, найти обратную матрицу для той же матрицы, что в задании 2.3.
Задание 2.7
Решить систему 3-х уравнений с 3-мя неизвестными по форму-
лам Крамера.
Расширенную матрицу системы взять из табл. 2.2. Значение главного определителя взять из решения задания 2.2.
Задание 2.8
Решить ту же систему, что в задании 2.7, матричным способом.
Обратную матрицу взять из решения задания 2.5.
Задание 2.9
Решить ту же систему, что в задании 2.7, методом Гаусса.
Таблица 2.2
К заданиям 2.2, 2.5, 2.7, 2.8, 2.9
 |
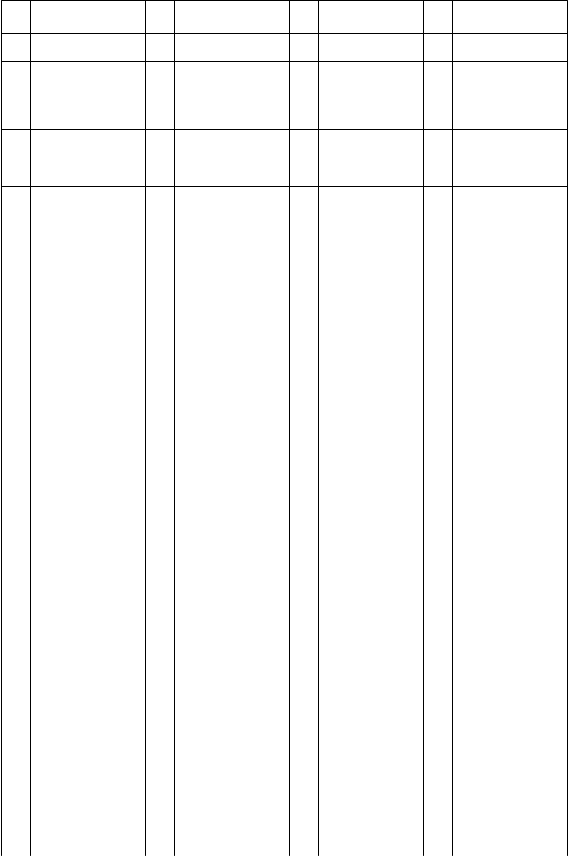n Ар n Ар n Ар n Ар
1 2 3 4 5 6 7 8
-1 -3 -3 -38 2 1 -5 -9 -2 2 -5 -20 -2 3 -3 -4
5 3 5 68 -1 -1 -2 -10 2 6 -3 4 -1 -2 4 10
1 -5 2 6 17 2 -3 -3 2 -6 3 -5 -5 3 -8 4 6 4 2 48
6 -3 1 -3 5 2 -1 18 2 1 3 15 1 -5 -2 -30
5 2 1 25 -1 -2 -3 -18 6 -2 2 14 -2 -5 5 -27
5 -5 4 6 32 6 -3 -2 1 -14 7 -2 -5 3 -5 8 -1 3 6 30
-2 -3 4 1 -3 2 5 12 1 -1 2 5 -2 -1 2 1
2 2 -5 -9 4 1 -1 23 6 4 1 37 3 4 1 31
9 2 3 5 44 10 2 3 2 34 11 -5 -3 1 -24 12 -5 -5 -1 -40
-5 2 2 -16 4 1 2 26 1 -2 -1 -3 6 -2 3 20
3 -1 -1 11 -5 1 -3 -29 5 -1 6 34 -5 -2 5 -9
13 -2 1 -2 -20 14 3 5 4 33 15 3 6 -3 27 16 -2 2 2 2
-2 -1 -1 -14 -5 -5 -5 -40 -1 -1 2 0 -2 -5 1 -16
-3 -1 -5 -36 -1 -3 4 -4 5 -1 3 27 -3 -1 -5 -37
17 3 1 2 21 18 -5 1 6 0 19 5 5 -1 27 20 -1 5 -3 -7
2 -2 -2 -6 -1 -3 -2 -14 6 -1 1 37 -1 -5 3 -14
6 3 1 23 2 6 2 22 6 -1 -5 13 -3 -2 -2 -34
21 3 1 5 19 22 -3 6 1 9 23 -5 2 -3 -36 24 -2 -2 -3 -32
1 1 3 14 1 1 2 11 5 -5 -3 -38 -2 -3 1 -11
4 -1 -2 3 -1 3 -5 -5 -5 -2 -3 -40 4 -2 1 10
25 1 -1 -3 -8 26 -1 -3 -3 -19 27 -5 -2 6 14 28 -3 1 -3 -18
1 1 5 39 -5 -5 4 -43 -3 -5 -2 -27 6 1 1 24
-3 4 -5 -22 6 -3 6 39 5 4 5 37 -3 4 -1 -5
29 3 1 6 53 30 2 4 1 35 31 -3 -5 -5 -36 32 -2 -3 -3 -24
5 3 3 44 1 2 3 23 -1 2 -1 -4 5 -2 2 36
-3 4 -1 -5 4 -2 1 9 1 -1 -2 -6 6 1 -3 21
33 3 -5 -1 -8 34 1 -3 5 4 35 -5 5 -2 -18 36 6 -5 -1 15
-5 -1 -3 -35 4 -5 1 15 -2 2 1 5 -3 2 1 -4
4 4 -3 2 4 -3 6 44 -2 6 -1 11 -1 -2 4 10
37 -5 3 -2 -21 38 -2 -1 -2 -22 39 -1 3 -2 -2 40 -5 1 2 -14
-5 -3 1 -10 6 1 -2 15 -2 -3 3 -10 2 2 -3 2
6 -1 4 34 -2 -3 4 7 -2 -3 -5 -50 4 -1 5 28
41 -5 -5 3 -2 42 3 5 1 33 43 3 -1 -3 -5 44 -2 4 -3 -2
-5 -1 6 5 6 -2 6 50 -1 -2 3 0 -1 -5 3 -13
-3 -3 -5 -52 -2 -1 -3 -23 2 -3 3 13 -3 -5 -1 -39
45 6 4 4 64 46 -3 -1 4 -8 47 6 6 3 51 48 -1 -5 -5 -45
6 1 -3 20 4 -3 2 20 5 -3 -2 18 6 -5 6 56
3 1 1 21 1 -5 -5 -20 5 4 -2 32 -5 5 5 5
49 -1 2 4 15 50 2 4 -1 15 51 -5 1 4 -16 52 -3 -2 -2 -32
Продолжение табл. 2.2
 | | | | |  | | | |
1 2 3 4 5 6 7 8
4 -3 2 10 -2 1 2 3 1 -2 5 6 5 1 1 21
3 -1 -2 3 -3 6 -2 -12 -3 -2 -5 -38 -1 1 2 6
53 -5 -2 -3 -25 54 -3 4 2 6 55 -3 -2 -2 -32 56 -1 5 3 21
2 -2 -2 -10 5 1 -1 22 1 2 6 36 6 -3 -5 -12
-3 4 1 13 -3 5 5 20 3 2 6 44 1 4 1 36
57 1 -5 -3 -37 58 5 -3 5 44 59 3 -1 -2 0 60 -2 2 1 6
-2 -2 -3 -22 6 2 -1 27 5 3 2 60 3 -5 -3 -12
-5 -3 4 -26 4 -2 -3 1 -3 -1 5 6 -5 1 3 -8
61 -5 5 -1 -12 62 6 -5 -5 -6 63 1 5 1 42 64 6 5 1 42
1 -5 -2 -22 1 -3 3 5 3 -2 6 30 -2 -2 6 -6
-5 4 3 12 3 -2 -1 -7 -1 -1 -3 -18 3 -1 6 19
65 5 -3 2 2 66 5 2 -5 -7 67 3 1 -3 12 68 -1 1 1 3
-2 1 2 0 -1 -5 3 -15 4 -1 2 27 1 -2 -1 -10
2 4 3 20 4 5 2 54 5 -1 2 33 -3 -2 1 -10
69 3 -3 5 13 70 1 1 -5 -21 71 -2 -3 -2 -27 72 -5 2 1 2
6 -5 5 40 -5 3 -1 -21 -1 -5 5 4 6 -3 -3 12
1 -3 -5 -21 -2 -3 -2 -29 5 3 5 56 5 -3 -2 10
73 3 6 -2 19 74 -2 2 4 16 75 1 1 4 24 76 1 -1 -5 -13
5 -1 -1 7 -1 -3 -2 -25 2 -2 -5 -29 -3 -2 -2 -34
4 -3 -1 -8 6 6 3 54 1 5 3 37 6 -2 -1 24
77 2 2 -3 12 78 3 -2 1 0 79 2 4 -1 15 80 2 -5 1 -4
1 1 1 10 5 1 6 37 -5 -1 2 -5 5 2 1 45
1 4 -2 4 1 -2 2 -2 2 -5 1 2 3 -1 -3 3
81 4 -2 -2 -8 82 -2 3 4 15 83 -3 -3 -5 -45 84 -3 4 4 18
-1 -2 6 7 5 2 5 31 6 -3 5 31 2 2 5 46
1 4 -2 21 5 5 -1 28 -5 1 2 2 3 -2 2 21
85 -2 -2 6 2 86 5 5 1 32 87 2 2 -3 -7 88 -2 4 3 20
-3 2 4 -1 3 -2 -2 -5 -3 -5 5 -11 -5 2 6 14
2 -5 5 5 5 1 6 65 3 2 2 16 5 5 1 49
89 1 -5 4 -2 90 2 4 4 50 91 -2 2 -2 -2 92 6 2 -2 26
2 1 4 30 -5 -2 5 -18 -2 1 -2 -8 6 -5 2 -10
-3 2 4 2 -5 -3 -1 -46 5 1 2 29 6 -2 2 8
93 -2 1 5 10 94 5 6 -3 42 95 -3 4 2 23 96 -1 3 2 24
-2 -1 4 5 1 -5 3 -1 4 2 6 46 -3 -3 1 -10
3 1 -5 -6 2 3 -2 10 -1 5 3 33 4 5 -5 -3
97 3 4 -1 25 98 -3 -5 -3 -47 99 3 5 -1 21100 -5 -1 5 8
|
Задание 2.10
Используя программное обеспечение ЭВМ, решить систему
4-х уравнений с 4-мя неизвестными А×Х = В.
Расширенную матрицу Ар = (А½В) коэффициентов системы
взять из табл. 2.3.
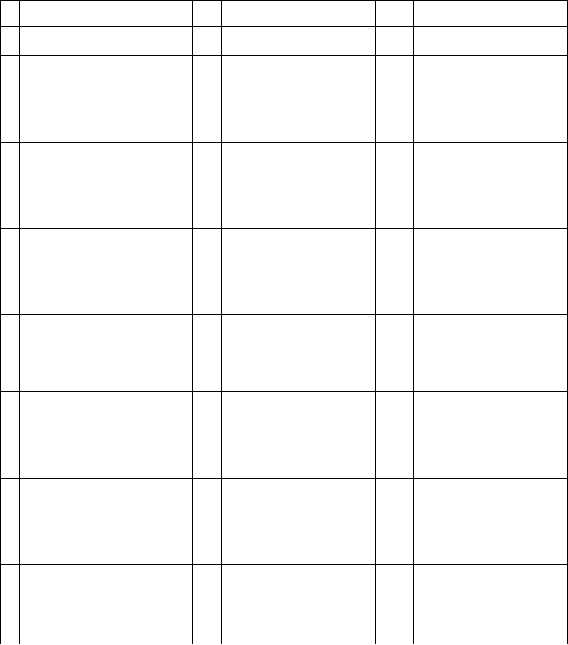
Таблица 2.3
К заданиям 2.3, 2.6, 2.10
 | |
 |
n Ар n Ар n Ар
1 2 3 4 5 6
2 4 -2 -5 5 2 -2 -5 3 -17 4 -5 -1 3 13
-5 4 1 2 11 2 1 2 -2 17 1 -2 1 -1 -4
2 1 4 4 44 -5 -2 -1 -2 -35 -2 1 1 1 5
1 2 -2 -1 4 16 2 4 2 -2 -1 10 3 -1 3 -5 -2 -30
3 3 -5 1 17 -2 4 -1 -5 -8 3 -1 2 -1 7
-1 -5 1 3 -9 -2 -5 1 3 -25 1 -1 2 -2 0
-5 -2 -5 -1 -44 -2 4 1 -5 4 -2 -1 -1 -1 -15
4 -5 4 2 2 -3 5 1 -2 2 -1 6 6 3 3 -2 3 19
-2 2 2 3 15 -1 3 2 -5 -1 3 1 -2 -5 -2
2 -1 -1 -5 -14 2 4 1 3 49 -2 4 -5 -2 -26
-1 2 3 4 25 -5 1 4 1 -3 -2 3 1 1 4
7 -2 2 2 1 9 8 -2 1 -5 4 -3 9 -5 -2 2 3 -19
-5 2 -5 -1 -49 1 -2 -1 3 2 3 -5 -5 1 -29
1 -1 2 4 20 -2 1 -2 3 0 -5 4 4 4 25
2 2 1 -5 15 1 4 4 -1 16 4 -2 2 2 8
10 2 3 -5 1 1 11 3 -5 4 4 12 12 -2 -5 -5 -1 -48
4 4 -5 -2 16 1 -2 -2 -5 -35 -2 -1 3 -2 -6
3 2 2 4 38 2 -1 2 -2 -4 2 -1 -1 -2 2
2 -2 4 -2 10 -5 -2 -2 -2 -35 2 -5 2 1 12
13 1 3 4 3 29 14 4 2 -2 -1 6 15 -5 -1 3 3 -14
-5 -2 1 -5 -43 2 4 3 2 54 2 3 -5 1 1
2 4 -5 1 10 3 -5 -5 -1 -35 1 3 -1 1 18
4 3 3 1 41 -1 -2 1 1 -11 -5 -5 -2 4 -47
16 2 -1 2 -1 10 17 4 -5 1 -1 -5 18 1 1 2 4 27
4 4 4 -2 26 2 -5 4 4 16 2 -5 -2 -5 -39
2 1 3 -1 12 1 -5 3 -5 -29 1 2 -1 4 29
-1 -5 -2 -1 -28 -2 4 -1 -2 4 -1 3 4 -1 17
19 3 -5 3 3 18 20 -5 1 -5 4 -23 21 1 -1 -5 2 -6
Продолжение табл. 2.3
1 2 3 4 5 6
2 -1 -1 3 6 2 -5 -1 3 -6 -1 3 -1 3 10
-5 -5 1 1 -25 3 3 3 1 32 4 -1 -2 2 14
-2 2 -1 1 -1 -2 1 -5 -5 -42 3 3 -5 4 20
22 1 -2 4 2 13 23 -5 -5 3 3 4 24 1 1 -1 2 10
-5 2 3 4 18 2 1 3 -2 11 2 2 2 -1 9
-5 2 -1 -5 -21 2 3 1 -2 13 2 -2 2 4 26
1 -2 -5 -5 -39 2 3 1 -5 4 -2 4 1 4 24
25 -1 2 -2 1 6 26 -1 2 4 4 22 27 1 1 4 1 18
-5 -5 2 3 -17 -5 3 -5 -5 -37 -2 -5 -2 -2 -37
3 -1 2 4 29 -2 2 -1 3 15 -1 3 3 -5 -6
-2 4 2 1 18 4 2 1 -2 17 3 -5 2 1 4
28 -2 -2 -2 4 -18 29 2 2 -5 -5 -29 30 1 1 3 -5 -8
3 -2 1 3 20 4 -1 -5 -1 -14 -1 -2 1 -5 -38
-1 2 -2 -2 -9 -5 3 3 3 12 3 -2 4 -2 2
-1 1 -5 1 -11 4 -5 3 3 42 -2 -5 4 -5 -51
31 2 1 -1 3 24 32 1 2 4 2 46 33 2 4 -5 -5 -8
4 1 -1 4 35 4 -1 -1 -1 -4 3 -1 4 1 18
4 2 1 4 43 1 -5 -2 3 2 4 2 2 2 34
-2 3 3 -5 -21 -2 4 3 2 28 4 4 1 1 35
34 -5 3 -2 -1 -21 35 -1 3 3 1 22 36 2 -1 -2 1 3
-2 -2 2 1 -10 -2 1 -1 3 5 -5 4 4 3 40
3 2 1 -1 21 -1 4 -5 4 -4 -1 -2 -2 -2 -36
3 4 -1 4 45 -1 -1 3 3 25 -2 1 -2 1 -10
37 -1 -5 4 1 -13 38 4 1 -5 3 -7 39 -1 3 1 1 24
1 1 -2 -5 -34 -2 4 2 -2 22 -2 1 -2 3 6
-1 -5 4 2 4 3 4 -5 1 1 -5 1 -1 4 7
3 -5 2 -5 -42 2 4 1 -5 22 3 3 3 2 35
40 2 3 -5 4 16 41 1 -2 1 2 3 42 2 2 -1 2 17
3 2 3 -1 19 -1 2 2 -2 1 -1 -2 2 -1 -8
3 2 -1 2 25 -1 -5 3 -1 -27 -2 2 3 2 26
-2 -2 3 -5 -33 1 4 1 -5 0 -5 2 2 -5 -40
43 1 -2 -1 -5 -33 44 2 3 1 -2 13 45 -5 -5 1 2 -32
-2 -5 2 2 -13 2 2 -5 2 17 4 -2 -5 -5 -11
-5 -2 2 -2 -33 4 -2 -2 4 22 2 -1 4 1 21
-2 -1 -2 2 -17 -1 2 -5 -5 -33 1 4 -5 -1 0
46 -1 -1 4 -5 -11 47 3 -1 -5 -2 -16 48 4 1 3 2 36
2 2 2 1 27 4 2 -2 3 25 -5 3 4 3 17
-5 4 -2 2 -12 3 3 2 -1 22 -2 4 2 4 22
4 -2 -1 -1 11 -2 -2 -1 -5 -31 3 2 -2 3 12
49 3 2 1 -5 1 50 2 -2 4 -2 0 51 2 -2 -1 -1 -7
Продолжение табл. 2.3
1 2 3 4 5 6
-2 1 4 2 31 -1 -5 4 -2 -15 -5 -5 2 1 -39
4 -2 3 2 28 -2 2 -5 2 -2 -5 -1 -1 1 -29
2 4 3 3 56 -5 2 4 -1 -8 -2 2 -1 3 2
52 -1 1 -1 1 0 53 -2 -2 2 4 14 54 -5 2 -1 3 -13
-1 1 1 -2 -6 -5 1 4 3 31 -2 1 -1 1 4
2 1 1 4 36 -2 2 -1 -2 -16 2 4 -1 3 39
2 -2 -2 3 7 2 1 -1 -2 -10 -2 3 3 1 26
55 4 -1 4 3 48 56 1 2 3 -5 -1 57 1 -1 1 1 6
3 -2 -1 2 5 3 -2 1 -5 -1 1 1 -5 1 -12
-2 -2 4 -2 -8 4 -1 -2 3 8 1 3 -5 -2 -21
-2 1 3 2 11 -1 -2 3 1 3 -1 -1 1 -5 -28
58 1 2 -2 4 15 59 -1 3 3 2 35 60 -5 -2 1 1 -21
-1 -5 1 1 -11 3 -5 1 4 18 4 4 2 -1 42
-1 -2 2 -5 -21 1 -2 1 -1 1 2 4 -5 -2 18
-2 3 -1 4 4 4 -1 -5 1 -3 -5 2 1 1 -4
61 2 -1 -5 -1 -3 62 1 3 -1 3 15 63 3 4 4 -5 34
4 4 -5 -5 -16 -2 -5 1 3 -12 2 -5 2 4 13
-1 1 4 1 12 3 -1 -5 4 16 -2 -5 4 2 -1
1 2 -5 -1 -8 -1 -1 3 3 18 2 2 3 1 25
64 4 1 3 2 36 65 -1 1 -5 -5 -44 66 -2 -2 -2 -5 -38
4 -1 2 -1 18 -2 -1 4 3 28 3 -5 4 -1 -4
-1 1 1 -5 -12 -1 -5 3 1 8 -2 1 -5 -1 -18
1 2 1 1 26 -2 -1 2 3 16 -5 -1 3 1 -14
67 2 -1 -2 4 6 68 -2 -1 -5 -1 -50 69 2 2 -5 4 22
4 1 1 -2 15 1 1 -5 -5 -20 -2 2 2 4 18
1 -2 -2 -2 -12 -2 -2 -2 -5 -29 -1 3 -1 3 12
-2 -1 3 3 8 3 2 1 -2 9 -5 2 2 2 -3
70 -1 1 1 -5 -14 71 3 -5 -5 3 -2 72 1 -1 1 3 14
3 -5 2 -2 1 3 2 2 4 40 2 1 -1 1 11
-1 -1 2 -2 -3 -5 4 3 -5 -20 1 -1 -1 -2 -12
2 2 -1 -2 3 -2 -1 4 1 10 1 4 1 1 32
73 -5 1 -5 -5 -57 74 1 4 -1 4 24 75 1 1 -1 -2 -2
-5 2 1 -5 -40 -1 4 3 -1 32 -5 -2 -1 -1 -31
1 -2 -2 4 16 3 3 -5 2 8 3 3 -1 2 33
4 3 -1 -1 20 1 -2 -1 -1 -16 -1 -1 3 2 13
76 2 -2 -1 4 22 77 1 -5 -5 -2 -52 78 4 -2 4 4 32
-5 4 -5 1 -32 1 3 2 1 28 -2 -1 2 -5 -28
-1 1 2 3 15 2 -1 -1 -2 -2 -5 2 2 4 29
-1 -2 3 -2 -2 -2 4 -5 -5 -15 1 4 4 -2 31
79 2 -1 4 -5 16 80 3 -1 -5 -2 -9 81 4 2 -1 4 38
Продолжение табл. 2.3
 |
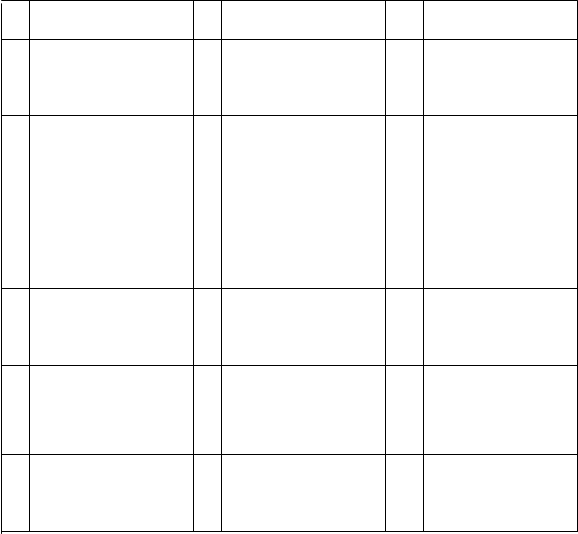1 2 3 4 5 6
1 -2 -5 4 -28 -2 4 -2 -5 -30 -1 4 -1 4 12
2 -2 2 4 16 -2 -2 1 -2 -30 -1 4 -2 3 3
3 -2 1 1 3 4 -2 3 3 40 1 1 -5 4 -9
82 -2 2 3 -5 11 83 2 -5 3 1 4 84 -5 3 -1 2 -21
2 -5 2 -2 -15 4 -2 2 -5 0 -2 -5 -5 4 -34
-5 -5 2 3 -18 -1 -2 1 3 -4 1 2 1 -5 -11
-5 4 -5 4 -10 2 2 -5 -1 -9 4 2 -2 3 34
85 2 -1 -2 1 -4 86 3 3 4 -1 45 87 1 -2 -1 -2 –23
-5 3 4 2 21 -2 1 -2 -5 -44 1 3 4 3 36
-1 -1 -2 -1 -20 3 2 4 -1 40 4 -5 -5 -5 -38
-2 -1 3 2 17 -2 -2 -2 2 -20 1 4 -5 -5 -2
88 -2 3 3 -5 -10 89 -2 3 1 -2 -2 90 -2 -1 1 -1 -10
4 4 4 -1 58 2 -2 -2 1 -9 -2 4 -5 -2 -6
1 1 1 -5 5 -5 -2 -2 4 -35 3 1 1 2 22
4 4 2 2 54 -5 -1 4 -5 -21 -5 4 2 -1 19
91 -5 1 3 4 3 92 4 3 2 -5 32 93 -2 2 -2 1 3
-2 2 -5 3 -8 -2 -1 -5 -5 -41 4 -1 4 4 27
-1 4 3 -2 21 -1 4 -5 2 8 4 -2 4 2 18
4 2 -5 -1 -4 3 3 -2 -5 17 4 1 3 -5 17
94 -2 -1 3 2 12 95 2 2 4 4 42 96 1 1 4 2 21
-1 -1 1 4 12 -5 1 4 -1 -1 4 -5 -1 3 -1
-2 2 1 2 10 -1 3 -2 -1 5 1 3 1 -1 25
3 1 -5 -1 -15 -5 4 -1 -1 2 -2 1 1 4 7
97 2 -5 -5 -5 -41 98 -2 1 4 -5 -8 99 -1 3 -5 -2 -25
Задание 2.11
Решить матричное уравнение А×Х×В + C = D.
Матрицы А, В, С, D взять из табл. 2.4.
Искать решение в следующем порядке: выразить из уравнения
неизвестную матрицу Х через известные А, В, С, D и обратные к
ним, затем вычислить обратные, подставить их в полученное вы- ражение и произвести действия в этом выражении.
Ответ проверить подстановкой в уравнение.
Задание 2.12
Решить матричное уравнение А×Х = Х×В + C.
Матрицы А, В, С взять из табл. 2.4.
Искать решение в следующем порядке: записать матрицу Х
с неизвестными коэффициентами: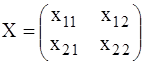 
. Выполнив
действия с матрицами в левой и правой частях уравнения, при-
равнять соответствующие коэффициенты матриц в левой и пра-
вой частях равенства. Получится система 4-х уравнений с 4-мя неизвестными. Для решения этой системы использовать ЭВМ.
Ответ проверить подстановкой в первоначальное матричное уравнение.
Таблица 2.4
К заданиям 2.11, 2.12.
 | |
| |
| |
|
Date: 2015-04-23; view: 479; Нарушение авторских прав