Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решение. Найдем уравнение прилежащего катета
|
|
|
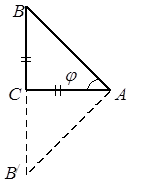
Найдем уравнение прилежащего катета. Так как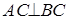 
, 
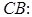
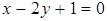, то уравнение 
имеет вид 
. 
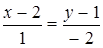
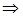
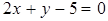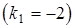Угол между катетом и гипотенузой в равнобедренном треугольнике 
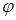равен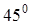 
. Для нахождения уравнения гипотенузы воспользуемся формулой 
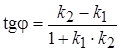, из которой найдем угловой коэффициент прямой 
.
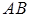1. 
.
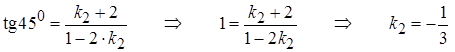Тогда уравнение 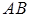имеет вид
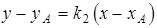
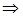
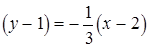
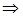
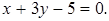
2. 
.
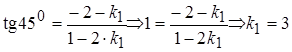Тогда уравнение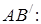 
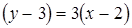
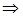
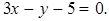
Ответ: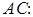 
, 
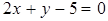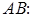
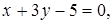
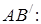
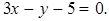
Прямая и плоскость в пространстве
Плоскость в декартовой системе координат может быть задана следующими уравнениями:
1. Общее уравнение плоскости
.
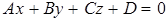Кроме того,
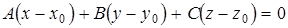
уравнение плоскости, которая проходит через точку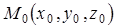 
перпендикулярно вектору 
.
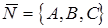2. Уравнение плоскости “в отрезках”
,
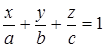где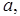 
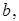
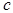– величины направленных отрезков, отсекаемых плоскостью на координатных осях 
, 
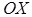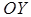и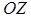 
, соответственно.
3. Уравнение плоскости, проходящей через три точки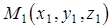 
, 
, 
.
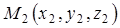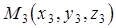
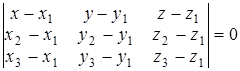Прямая в пространстве задается:
1) общими уравнениями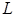 
в пространстве в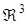 
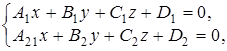
где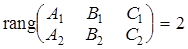 
, таким образом, прямая задана как линия пересечения двух плоскостей.
2) каноническими уравнениями 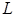в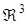
,
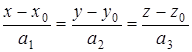где 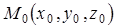– точка, принадлежащая прямой, а 
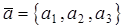– направляющий вектор.
3) параметрическими уравнениями
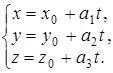
Пример. Составить уравнение плоскости, проходящей через точку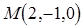 
и прямую 
.
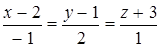Date: 2015-06-05; view: 720; Нарушение авторских прав