Вопрос 1

Что понимается под названием вычислительный эксперимент?

Коротко говоря – создание и изучение математических моделей исследуемых объектов с помощью ПЭВМ

Уместно ли здесь слово «эксперимент». Безусловно. При математическом моделировании мы имеем дело не с самим явлением, а с некоторым теоретическим «слепком» с него, с моделью, выражающей в математической форме основные закономерности, которым она подчиняется. В результате исследователь, проводя вычислительный эксперимент, испытывает как бы саму природу (конструкцию, технологический процесс, объект вооружения, операцию), задавая ей вопросы и получая строгие и относительно полные ответы.

Возможность замены исходного объекта его математической «концепцией» и дальнейшего «диалога» с нею таит в себе большие преимущества и означает серьезное изменение методологии и технологии военно-научных исследований. Становится все более ясной неизбежность широкого использования математического моделирования для реализации государственных комплексных научно-технических программ вообще и программ развития отраслей в частности.

Концепция вычислительного эксперимента (его также называют методом статистических испытаний) в настоящее время детально разработана и очерчена сфера его приложения.

Он имеет свои особенности в различных областях науки и предназначен для изучения, прогнозирования, оптимизации сложных многопараметрических стохастических нелинейных процессов, теоретическое и экспериментальное исследование которых традиционными методами затруднено или невозможно (например, прогнозирование хода и исхода боевых действий, задачи баллистики, эргономики и т.д.).

Метод статистических испытаний – один из основных методов моделирования больших систем. Широкое применение метода объясняется тем, что он позволяет заменить эксперимент с реальной системой экспе­риментом с моделью этой системы на ПЭВМ. При моделировании методом статистических испытаний не требуется строгого матема­тического описания системы: достаточно знать в общих чертах ал­горитм ее функционирования. Этот алгоритм может быть задан описательно и переведен в машинную программу.

Во многих прак­тических задачах построение математической модели функциони­рования системы в целом трудно осуществимо, но можно аналитически описать поведение отдельных элементов и построить моделирующий алгоритм функционирования системы, реализуемый на ПЭВМ. В этих случаях статистическое моделирование оказывается единственно приемлемым средством исследования.

Статистическое моделирование представляет собой численный метод исследования модели системы. Строго говоря, ПЭВМ не яв­ляется принципиально обязательным инструментом метода. Одна­ко огромное количество вычислений, которое при этом требуется выполнить, делает возможным практическое применение метода только с помощью ПЭВМ.

Сущность метода состоит в имитации на ПЭВМ случайных про­цессов, протекающих в реальной системе, с учетом структуры си­стемы, связей и взаимовлияний между ее элементами. Имитация осуществляется реализацией соответствующего моделирующего алгоритма.

Вследствие того, что моделируемый процесс является случай­ным, результаты, полученные при однократном моделировании, не могут характеризовать его. Искомые величины, характеризующие исследуемый процесс, находят статистической обработкой данных, полученных многократным моделированием. Если число испытаний достаточно велико, то в силу закона больших чисел полученные оценки приобретают статистическую устойчивость и с достаточной для практики точностью могут быть приняты в качестве характеристик процесса.

Пусть моделируется процесс, зависящий от случайных параметров 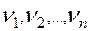. Законы распределения вероятностей этих параметров известны. В каждом из независимых испытаний получается некоторая величина 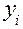, где 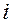– номер испытания. Требуется определить характеристики процесса. Ход моделирования – метод статистических испытаний можно представить следующим образом. Строится модель, описывающая структуру и функционирование системы с учетом связей и взаимовлияний между ее элементами, на основе модели строится моделирующий алгоритм.

Следующим шагом является моделирование случайных параметров системы. Например, параметр 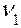может быть распределен по нормальному закону с математическим ожиданием 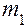и дисперсией , параметр – также по нормальному закону с математическим ожиданием 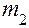и дисперсией 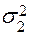, параметр 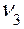– равномерно в интервале 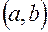и т. д.

Далее производится испытаний. В результате каждого испытания получают случайное значение 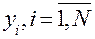. Значения 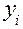запоминаются и используются для вычисления величин, характеризующих процесс функционирования системы. Для обеспечения статистической устойчивости эти величины определяются как средние значения по большому числу испытаний . Выбор зависит от требований точности, предъявляемых к результатам моделирования.

Таким образом, можно выделить три основные составные части метода статистических испытаний:

1) построение математической модели и моделирующего алгоритма исследуемой системы;

2) формирование случайных величин с заданным законом распределения вероятностей;

3) статистическая оценка результатов моделирования.

Нельзя указать общих правил построения модели и моделирующего алгоритма. Однако имеются приемы, позволяющие представить формализованный процесс функционирования системы в виде последовательности операций (или групп операций), выполняемых ПЭВМ. В качестве примера далее будет рассмотрено построение структуры алгоритма, моделирующего работу системы массового обслуживания (СМО). Методы формирования случайных величин с заданным законом распределения излагаются в следующем параграфе. Здесь же рассмотрим вопросы оценки точности метода статистических испытаний и определения необходимого числа испытаний .

Статистическая обработка и оценка точности результатов моде­лирования основывается на предельных теоремах теории вероят­ностей: теореме Чебышева и теореме Бернулли.

Согласно теореме Чебышева, при неограниченном увеличении числа независимых испытаний среднее арифметическое значение 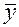случайной величины 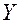сходится по вероятности к математическому ожиданию 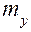этой величины, то есть

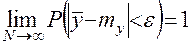, (1)

где 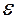– сколь угодно малое положительное число,

.

Теорема Бернулли доказывает, что при неограниченном увеличении числа независимых испытаний частота 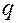наступления случайного события сходится к вероятности 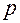этого события, то есть

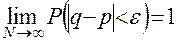. (2)

Пусть случайная величина 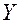характеризуется математическим ожиданием 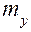и дисперсией 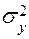. В качестве приближенного значения величины 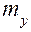берется среднее арифметическое значение 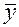, определяемое по результатам независимых испытаний. Отклонение величины 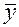от искомого математического ожидания 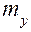и есть ошибка метода. Величина 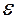, удовлетворяющая неравенству 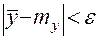, называется точностью оценки.

Из теоремы Чебышева следует, что ошибка метода может быть оценена лишь вероятностно, с определенной степенью достоверности. Обозначим через вероятность того, что выполняется неравенство :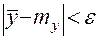

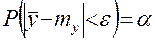. (3)

Вероятность характеризует степень достоверности оценки, ее надежность. Это означает, что с надежностью можно быть уверенным, что среднее арифметическое значение 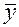не выйдет за пределы интервала 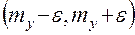, то есть, что

.

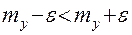Вероятность называют доверительной вероятностью, а границы интервала 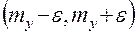, в которых с заданной доверительной вероятностью заключена ошибка метода – доверительными границами.

Из теории вероятностей известно, что при нормальном законе распределения вероятность отклонения случайной величины 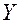от ее математического ожидания 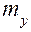менее, чем 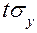на равна

, (4)

где – функция Лапласа (интеграл вероятностей);

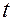– аргумент функции Лапласа;

– среднее квадратическое отклонение величины .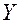

Также известно, что если производится большое число опытов, то среднее арифметическое 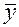есть также случайная величина, приближенно распределенная по нормальному закону с математическим ожиданием 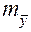и средним квадратическим отклонением .

Из сказанного следует, что вероятность любого отклонения 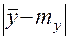может быть вычислена по формуле [2]

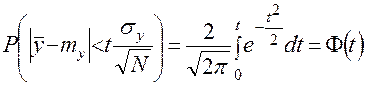. (5)

Положим

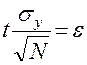, (6)

тогда получим

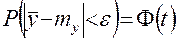. (7)

Сравнивая выражения (3) и (7), найдем условие, при котором ошибка метода не превысит величину 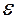с вероятностью :

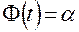. (8)

Задаваясь доверительной вероятностью , найдем из уравнения (8) с помощью таблиц функции Лапласа численное значение . Подставив далее величину 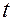в выражение (6), получим формулу для вычисления искомого числа испытаний , при кото­ром выполняется условие (8):

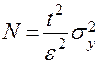. (9)

Из формулы (9) видно, что для определения необходимо еще знать величину дисперсии 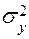. Так как она неизвестна, обычно поступают следующим образом. Задаются некоторым достаточно большим значением 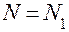и находят приближенное значение (статистическую оценку) дисперсии по формуле

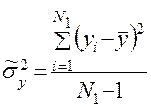. (10)

Величину 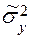подставляют в формулу (9) и находят уточнен­ное значение . Таким образом, достигаемая точность может быть хорошо оценена только в процессе моделирования.

Задавая доверительную вероятность , получаем из формул (5), (8) доверительную оценку

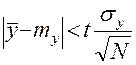(11)

с надежностью . Отсюда вытекает, что ошибка метода статисти­ческих испытаний пропорциональна величине 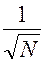. Следовательно, чтобы уменьшить ошибку в 10 раз (то есть, чтобы получить в ответе еще один верный знак), нужно увеличить число испытаний в 100 раз. Чтобы получить достаточно высокую точность, необходимо провести тысячи испытаний. Метод особенно эффективен при реше­нии задач, в которых результат нужен с точностью порядка 5 – 10 %.

Мы рассмотрели точность моделирования процесса, в котором при каждом из независимых испытаний получается величина 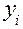, имеющая математическое ожидание 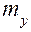. Рассмотрим теперь слу­чай моделирования события 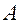, вероятность появления которого в каждом из независимых испытаний равна 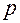. Обозначим через 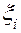величину, равную единице, если на 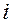-м испытании произошло событие 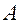, и равную нулю, если событие 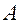не произошло. Следовательно, общее число испытаний, в каждом из которых событие 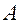произошло, равно 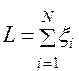, а частота появления события равна .

Так как 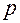есть искомая величина, а 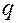– ее приближенное значение, то 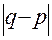есть ошибка метода.

Введя снова величину 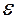, удовлетворяющую неравенство 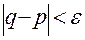, и доверительную вероятность , получим на основании теоремы Бернулли

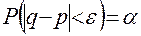. (12)

Можно показать, что в этом случае необходимое число испытаний определяется по формуле

, (13)

где 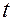также находится из условия (8).

Так как до начала испытаний величина 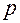неизвестна, то в формулу (13) вместо 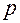подставляют значение частоты 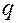, вычисленное при достаточно большом числе испытаний 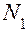, и определяют уточненное значение .

Основными достоинствами метода статистических испытаний являются:

· применимость для моделирования очень сложных систем и процессов любой физической природы. Система может содержать элементы непрерывного и дискретного действия, быть подверженной воздействию многочисленных случайных факторов, описываться сложными линейными и нелинейными зависимостями и т. д.;

· простота осуществимости. Составляется программа для одного испытания, затем испытание повторяется раз. Нет необходимости в создании специальных устройств;

· простота оценки точности полученных результатов.

Наиболее существенным недостатком метода, ограничивающим его применение, является большое количество испытаний, которые необходимо провести для получения характеристик исследуемой системы с высокой точностью.

Кроме того, методу присущ общий недостаток любых численных методов, связанный с трудностями установления функциональных зависимостей между параметрами системы. Это объясняется тем, что результаты каждого испытания носят частный характер и характеризуют поведение системы лишь для тех значений параметров, при которых проводилось моделирование.

Date: 2015-05-23; view: 601; Нарушение авторских прав