
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Моделирование системы массового обслуживания
|
|
Методы теории массового обслуживания применяются для исследования функционирования широкого класса систем. Однако ее аналитический аппарат позволяет получить достаточно полные результаты для сравнительно простых случаев.
Метод статистических испытаний дает возможность более полно, по сравнению с аналитическими методами, характеризовать зависимость качества функционирования системы от параметров потока заявок и обслуживающей системы. При этом он допускает более широкие предположения о природе потоков заявок, структуре обслуживающей системы и дисциплине обслуживания, чем аналитические методы. Например, он позволяет получить решение задач для многофазных систем при весьма общих предположениях об их структуре; доступных же аналитических методов исследования многофазных систем в настоящее время нет.
Применение метода статистических испытаний для моделирования процесса функционирования системы массового обслуживания рассмотрим на конкретном примере системы с отказами.
Система, в которую в отдельные случайные моменты времени поступают заявки, состоит из 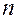 каналов (пунктов обслуживания). Поток заявок представляет собой простейший поток, интервал времени
каналов (пунктов обслуживания). Поток заявок представляет собой простейший поток, интервал времени 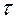 между двумя последовательными событиями есть случайная величина, распределенная по экспоненциальному закону, и вычисляется по формуле:
между двумя последовательными событиями есть случайная величина, распределенная по экспоненциальному закону, и вычисляется по формуле:
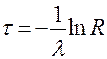 ,
,
где 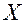 – интенсивность потока заявок (среднее число заявок в единицу времени);
– интенсивность потока заявок (среднее число заявок в единицу времени);
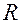 – случайная величина, равномерно распределенная в интервале
– случайная величина, равномерно распределенная в интервале 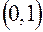 .
.
Каждая заявка поступает для обслуживания в канал, который освободился раньше всех. Если есть каналы, освободившиеся одновременно, заявка поступает в канал с меньшим номером. Время обслуживания 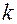 -й заявки
-й заявки 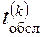 является случайной величиной, равномерно распределенной в интервале
является случайной величиной, равномерно распределенной в интервале 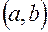 , и вычисляется по формуле:
, и вычисляется по формуле:
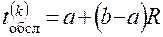 .
.
Если в момент поступления заявки все каналы заняты, система выдает отказ.
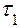 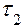 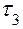 
            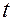
 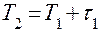
 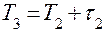
 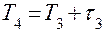
 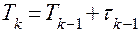
 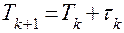
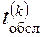
  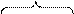  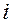 -й канал -й канал 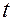
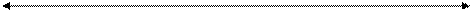 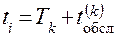 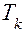
|
Рис.2.1. Показатели эффективности системы за время функционирования 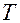
Требуется определить показатели эффективности системы за время функционирования 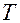 .
.
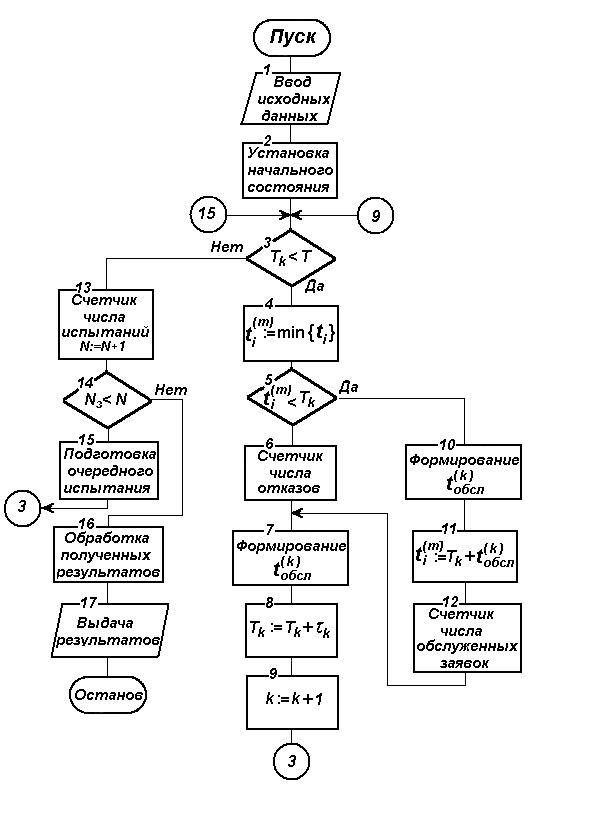
Рис. 2.2. Логическая схема алгоритма процесса обслуживания заявок
Введем следующие обозначения (рис. 2.1):
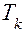 – момент поступления
– момент поступления 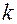 -й заявки;
-й заявки;
 –
– 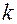 -й интервал между двумя последовательными заявками (между
-й интервал между двумя последовательными заявками (между 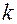 -й и
-й и 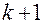 заявками);
заявками);
 – момент освобождения
– момент освобождения 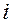 -го канала:
-го канала:
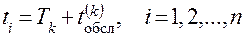
За начальный примем момент поступления первой заявки 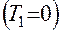 .
.
В этот момент все каналы свободны 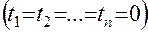 .
.
На рис. 2 изображена логическая схема алгоритма, моделирующего процесс обслуживания заявок рассмотренной системы. Каждый оператор представляет, как правило, подалгоритм, реализующий в процессе моделирования определенную функцию системы.
Оператор 1 осуществляет ввод исходной информации: число каналов системы 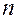 , параметры законов распределения потока заявок и времени обслуживания
, параметры законов распределения потока заявок и времени обслуживания 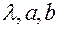 , время работы системы
, время работы системы 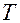 , заданное число испытаний
, заданное число испытаний 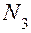 .
.
Оператор 2 устанавливает перед началом каждого испытания значения 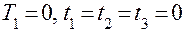 и
и  . Тем самым устанавливает начальное состояние системы и фиксируется факт появления первого требования.
. Тем самым устанавливает начальное состояние системы и фиксируется факт появления первого требования.
Оператор 3 определяет, принадлежит ли 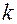 -я заявка заданному интервалу времени
-я заявка заданному интервалу времени 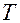 функционирования системы. Если условие
функционирования системы. Если условие 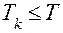 выполняется, заявка поступает на обслуживание, управление передается оператору 4. В противном случае испытание заканчивается и управление передается на счетчик числа испытаний.
выполняется, заявка поступает на обслуживание, управление передается оператору 4. В противном случае испытание заканчивается и управление передается на счетчик числа испытаний.
Оператор 4 сравнивает между собой моменты освобождения каналов системы и выбирает канал, освободившийся раньше всех. Если есть каналы, освободившиеся одновременно, выбирается канал с меньшим номером. Пусть номер выбранного канала равен 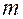 . Заявка поступает для обслуживания в этот канал. Очевидно, в каждом испытании первая заявка поступает в первый канал, вторая заявка – во второй канал, третья – в третий, так как в начальный момент
. Заявка поступает для обслуживания в этот канал. Очевидно, в каждом испытании первая заявка поступает в первый канал, вторая заявка – во второй канал, третья – в третий, так как в начальный момент 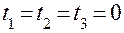 .
.
Оператор 5 сравнивает момент освобождения выбранного канала 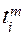 с моментом поступления
с моментом поступления 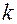 -й заявки
-й заявки 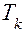 . Если условие
. Если условие 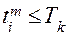 не выполняется, это означает, что все каналы к моменту
не выполняется, это означает, что все каналы к моменту 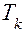 заняты, система выдает отказ и управление передается оператору 6. Если же указанное условие выполняется, канал с номером
заняты, система выдает отказ и управление передается оператору 6. Если же указанное условие выполняется, канал с номером 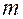 свободен и управление передается оператору 10.
свободен и управление передается оператору 10.
Оператор 6 представляет собой счетчик числа отказов, после каждого отказа показание счетчика увеличивается на единицу.
После отказа 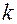 -й заявке необходимо формировать следующую заявку. Для этой цели предназначены операторы 7, 8 и 9.
-й заявке необходимо формировать следующую заявку. Для этой цели предназначены операторы 7, 8 и 9.
Оператор 7 формирует поток заявок, то есть по формуле
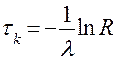
определяет интервал времени между двумя последовательными заявками (между 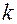 -й и
-й и 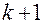 ). Из формулы видно, что для определения
). Из формулы видно, что для определения  оператор также формирует значения
оператор также формирует значения 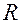 .
.
Оператор 8 формирует момент поступления следующей заявки
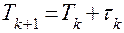 .
.
Оператор 9 формирует номер очередной заявки (за новым номером сохраняется прежнее обозначение 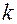 ). С оператора 9 управление передается на оператор 3, где момент поступления новой заявки (за ним сохраняется прежнее обозначение
). С оператора 9 управление передается на оператор 3, где момент поступления новой заявки (за ним сохраняется прежнее обозначение 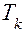 ) сравнивается с временем
) сравнивается с временем 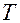 , и начинается новый цикл.
, и начинается новый цикл.
Если условие 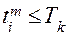 , проверку которого осуществляет оператор 5, выполняется, то выбранный оператором 4 канал с номером
, проверку которого осуществляет оператор 5, выполняется, то выбранный оператором 4 канал с номером 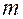 свободен и заявка передается в этот канал для обслуживания. Дальше необходимо определить время обслуживания
свободен и заявка передается в этот канал для обслуживания. Дальше необходимо определить время обслуживания 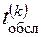
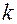 -й заявки, найти время освобождения канала, зафиксировать обслуженную заявку и формировать следующую заявку. Эту задачу выполняют операторы 10, 11 и 12.
-й заявки, найти время освобождения канала, зафиксировать обслуженную заявку и формировать следующую заявку. Эту задачу выполняют операторы 10, 11 и 12.
Оператор 10 определяет время обслуживания 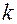 -й заявки согласно формуле
-й заявки согласно формуле
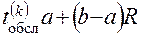 .
.
Оператор 11 вычисляет время освобождения 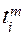 канала с номером
канала с номером 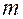 по формуле
по формуле
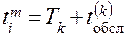 .
.
Оператор 12 представляет собой счетчик числа обслуженных заявок, после каждой обслуженной заявки показание счетчика увеличивается на единицу.
С оператора 12 управление передается на оператор 7 и дальше формируется следующая заявка так же, как и в рассмотрением случае отказа в обслуживании.
Если неравенство 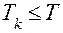 не выполняется (следовательно
не выполняется (следовательно 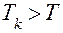 , это означает, что
, это означает, что 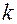 -я заявка уже не принадлежит заданному интервалу, и реализация на этом заканчивается.
-я заявка уже не принадлежит заданному интервалу, и реализация на этом заканчивается.
Оператор 13 представляет собой счетчик числа испытаний.
Оператор 14 проверяет, получено ли уже заданное число испытаний 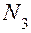 . Если неравенство
. Если неравенство 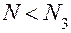 выполняется, управление передается оператору 15.
выполняется, управление передается оператору 15.
Оператор 15 осуществляет подготовку к следующему испытанию. При этом очищаются рабочие ячейки, хранящие значения 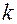 и
и  , а содержимое ячеек, хранящих число отказов и обслуженных заявок, пересылаются в специальный массив для последующей статистической обработки. Дальше управление передается на оператор 3, и начинается очередное испытание.
, а содержимое ячеек, хранящих число отказов и обслуженных заявок, пересылаются в специальный массив для последующей статистической обработки. Дальше управление передается на оператор 3, и начинается очередное испытание.
Если неравенство 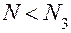 не выполняется, управление передается оператору 16.
не выполняется, управление передается оператору 16.
Оператор 16 осуществляет статистическую обработку полученных результатов и вычисляет требуемые показатели эффективности функционирования системы за время 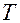 .
.
Можно моделировать работу системы за целый месяц в течение нескольких минут машинного времени. Преимущество «сжатия времени» при моделировании становится очевидным, если попытаться получить такую же информацию, используя физическую систему.
Пример. Рассмотрим, как можно моделировать однофазные системы обслуживания с помощью ручных вычислений. Этот пример должен пояснить основные идеи, описанные выше.
Пусть мы хотим моделировать систему массового обслуживания, поступление требований в которой подчинено пуассоновскому распределению со средним 3 клиента в час, а время обслуживания равно 0,2 ч с вероятностью 0,5 или 0,6 ч с вероятностью 0,5. Клиенты обслуживаются согласно дисциплине «первым пришел – первым обслуживаешься»; длина очереди, а также источник поступления клиентов не ограничены. Предположим, что в начальный момент моделирования клиентов нет.
Для пуассоновского входного потока со средней интенсивностью 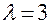 клиента в час промежутки времени между требованиями имеют экспоненциальное распределение и, как показано ранее, могут быть получены из формулы
клиента в час промежутки времени между требованиями имеют экспоненциальное распределение и, как показано ранее, могут быть получены из формулы
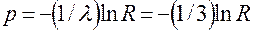 .
.
Поскольку время обслуживания равно либо 0,2, либо 0,6 ч с равными вероятностями, время обслуживания определяется как
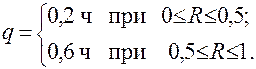
Как указывалось выше, в однофазной системе обслуживания возможны события только двух типов: поступление клиентов и их уход (окончание обслуживания). Действия, вызываемые этими событиями, можно охарактеризовать следующим образом.
Date: 2015-05-23; view: 735; Нарушение авторских прав