Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задачи. 2.56. Написать уравнение плоскости Р¢, проходящей через точку М параллельно заданной плоскости Р
|
|
2.56. Написать уравнение плоскости Р ¢, проходящей через точку М параллельно заданной плоскости Р, и вычислить расстояние между Р и Р ¢, если:
а) Р: –2 x + y – z + 1 = 0, M (1, 1, 1);
б) Р: x – y – 1 = 0, M (1, 1, 2).
2.57. Написать уравнение плоскости Р ¢, проходящей через заданные точки М 1 и М 2 перпендикулярно заданной плоскости Р, если:
а) Р: - x + y – 1 = 0, M 1(1, 2, 0), M 2(2, 1, 1);
б) Р: 2 x – y + z + 1 = 0, M 1(0, 1, 1), M 2(2, 0, 1).
2.58. Написать уравнение плоскости, проходящей через точку М параллельно векторам а 1 и а 2, если:
а) M (1, 1, 1), а 1(1, 2, 0), а 2(2, 1, 1);
б) M (0, 1, 2), а 1(0, 1, 1), а 2(2, 0, 1).
2.59. Написать уравнение плоскости, проходящей через заданные точки М 1 и М 2 параллельно вектору а, если:
а) а (3, 0, 1), M 1(1, 2, 0), M 2(2, 1, 1);
б) а (0, –1, 2), M 1(0, 1, 1), M 2(2, 0, 1).
2.60. Написать уравнение плоскости, проходящей через три заданные точки М 1, М 2 и М 3, если:
а) M 1(1, 2, 0), M 2(2, 1, 1), M 3(3, 0, 1);
б) M 1(1, 1, 1), M 2(0, –1, 2), M 3(2, 3, –1).
2.61. Исследовать взаимное расположение заданных плоскостей Р 1 и Р 2. Если плоскости параллельны, то найти расстояние между ними. Если плоскости пересекаются, то найти косинус угла между ними:
а) Р 1: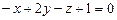 
, Р 2: 
;
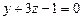б) Р 1: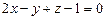 
, Р 2: 
;
в) Р 1: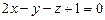 
, Р 2: 
.
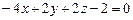2.62. Найти расстояние от точки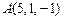 
до плоскости 
.
2.63. Найти расстояние между параллельными плоскостями:
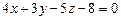и 
.
2.64. Написать уравнение плоскости, проходящей через точку 
и перпендикулярной к плоскостям 
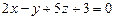и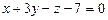 
.
2.65. Написать канонические и параметрические уравнения прямой, проходящей через две заданные точки М 1 и М 2, если:
а) M 1(1, –2, 1), M 2(3, 1, –1); б) M 1(3, –1, 0), M 2(1, 0, –3).
2.66. Прямая задана общими уравнениями. Написать для этой прямой канонические уравнения, если:
а) 
б)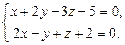 
2.67. Найти расстояние между параллельными прямыми:
и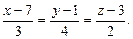 
2.68. Доказать, что прямые параллельны и найти расстояние между ним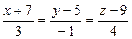и: 
и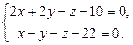 
2.69. Доказать, что прямые пересекаются и найти точку их пересечения: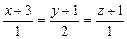 
и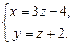 
2.70. Найти угол между прямым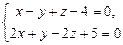и:
и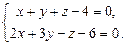 
2.71. Написать уравнение прямой, проходящей через точки пересечения плоскости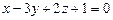 
с прямым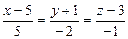и:
и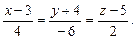 
2.72. Через прямую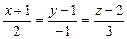 
провести плоскость, параллельную прямой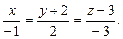 
Date: 2015-04-23; view: 971; Нарушение авторских прав