Раздел I. Линейная алгебра

1. Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная).

2. Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.

3. Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц.

4. Определители 2-ого и 3-егопорядка, их вычисление. Основные свойства определителей.

5. Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца.

6. Понятие системы линейных алгебраических уравнений (СЛАУ). Частные виды СЛАУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛАУ.

7. Решение, множество решений СЛАУ. Совместность, несовместность, определённость, неопределённость, эквивалентность СЛАУ. Элементарные преобразования СЛАУ, их основное свойство.

8. Метод Крамера для решения СЛАУ и условия его применимости.

9. Метод Гаусса решения СЛАУ и условия его применимости. Условия несовместности, определённости и неопределённости СЛАУ по методу Гаусса.

10. Преобразования СЛАУ, выполняемые при выполнении прямого и обратного ходов метода Гаусса. Базисные и свободные переменные. Нахождение общего решения СЛАУ. Частные решения СЛАУ.

11. Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы (метод присоединённой матрицы).

12. Матричные уравнения и их решение.

13. Матричная форма записи СЛАУ. Матричный способ (метод обратной матрицы) решения СЛАУ и условия его применимости.

14. Однородные СЛАУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛАУ.

15. Понятие линейной независимости и зависимости частных решений однородной СЛАУ. Понятие фундаментальной системы решений (ФСР). Представление общего решения однородной СЛАУ через ФСР.

16. Минор 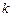-ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛАУ (теорема Кронеккера-Капелли).

17. Понятие 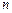-мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.

18. Скалярное произведение арифметических векторов. Понятие ортогональности векторов.

19. Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов.

20. Понятие векторного пространства 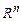, евклидова пространства 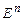. Базис, канонический базис и ранг .

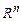21. Разложение вектора в 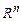по векторам его базиса. Теорема о единственности разложения вектора в данном базисе. Координаты вектора в .

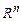22. Понятие ортогональной системы векторов, ортогонального базиса. Нахождение координат вектора в ортогональном базисе.

23. Понятие оператора, линейного оператора. Матрица линейного оператора. Сумма (разность) операторов, произведение оператора на число, произведение операторов, обратный оператор.

24. Понятие собственного числа и собственного вектора матрицы (линейного оператора). Характеристическое уравнение. Нахождение собственных чисел и собственных векторов матрицы (линейного оператора).

25. Понятие квадратичной формы. Матрица квадратичной формы. Виды квадратичных форм (вырожденная, невырожденная, каноническая). Преобразование квадратичной формы при линейном преобразовании переменных. Закон инерции квадратичных форм.

26. Понятие знакоопределённости квадратичной формы. Главные миноры матрицы квадратичной формы. Критерии знакоопределённости квадратичной формы.