Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задачи. 2.1. В треугольнике ABC: , точка M – середина стороны BC
|
|
2.1. В треугольнике ABC: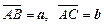 
, точка M – середина стороны BC. Выразить вектор 
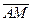через векторы a и b.
2.2.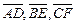 
– медианы треугольника ABC. Доказать равенство 
.
2.3.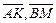 
– медианы треугольника ABC. Выразить через 
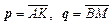векторы 
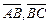и 
.
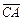2.4. Доказать, что средняя линия треугольника параллельна его основанию и длина ее равна половине длины основания.
2.5. Доказать, что сумма векторов, соединяющих центр правильного треугольника с его вершинами, равна нулю.
2.6. Даны векторы a и b, угол между которыми 120о. Построить вектор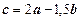 
и определить его модуль, если 
.
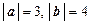2.7. На плоскости заданы векторы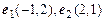 
и 
. Убедиться, что 
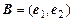– базис на множестве всех векторов на плоскости. Найти разложение вектора a по базису B.
2.8. Показать, что тройка векторов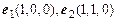 
, 
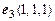образует базис на множестве всех векторов пространства. Вычислить координаты вектора 
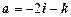в базисе 
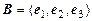и написать соответствующее разложение по базису.
2.9. Найти вектор x, коллинеарный вектору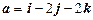 
и имеющий длину 
.
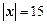2.10. Могут ли векторы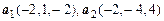 
и 
быть сторонами треугольника?
2.11. Коллинеарны ли векторы a и b, если коллинеарны векторы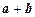 
и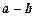 
?
2.12. При каких значениях a и b векторы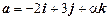 
и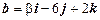 
коллинеарны?
2.13. Вычислить расстояние между точкам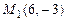и 
и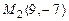 
и расстояние от точки 
до начала координат.
2.14. Вычислить периметр треугольника с вершинами в точках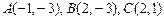 
.
2.15. Показать, что треугольник ABC с вершинами 
– прямоугольный.
2.16. Даны три вершины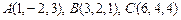 
параллелограмма ABCD. Найти его четвертую вершину D, противоположную B.
2.17. Даны две смежные вершины параллелограмма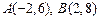 
и точка пересечения его диагоналей 
. Найти две другие вершины.
2.18. На оси абсцисс найти точку M, расстояние от которой до точки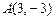 
равно 5.
2.19. На оси ординат найти точку M, равноудаленную от точек
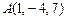и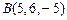 
.
Date: 2015-04-23; view: 1035; Нарушение авторских прав