Линейная зависимость векторов. Базис

Векторы 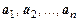называются линейно зависимыми, если существуют действительные числа a ₁, a ₂, …, a_n, из которых, по меньшей мере, одно отлично от нуля, такие что

.

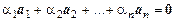В противном случае (т. е. когда таких чисел не существует) векторы называются линейно независимыми; другими словами, векторы линейно независимы, если последнее равенство выполняется лишь в случае, когда

.

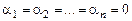Сформулируем несколько основных свойств линейной зависимости векторов.

1. Векторы 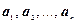линейно зависимы тогда и только тогда, когда, по меньшей мере, один из них является линейной комбинацией остальных.

2.Два вектора a и b линейно зависимы тогда и только тогда, когда они коллинеарны.

3. Есл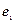и и 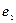– два неколлинеарных вектора некоторой плоскости, то любой третий вектор этой же плоскости можно единственным образом разложить по ним, т.е. представить в виде

.

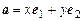4. Три вектора 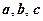линейно зависимы тогда и только тогда, когда они компланарны.

5. Если векторы 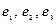некомпланарны, то любой вектор a в пространстве можно единственным образом разложить по ним, т.е.

.

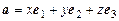6. Всякие четыре вектора в пространстве линейно зависимы.

В пространстве любая упорядоченная система трех линейно независимых (т.е. некомпланарных) векторов 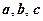называется базисом. Согласно свойству 5, всякий вектор d можно разложить по базису, т.е. представить в виде

.

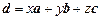Числа 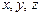называют координатами вектора d в базисе .

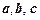Базис (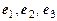) называется прямоугольным, если векторы 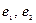и 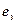попарно перпендикулярны и имеют единичную длину. В этом случае приняты обозначения:

.

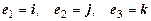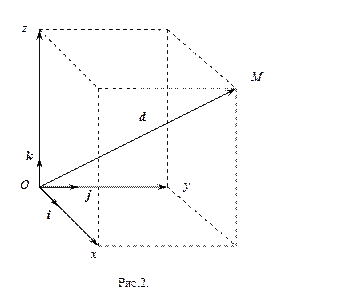
Координаты 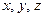вектора 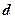в прямоугольном базисе совпадают с проекциями вектора 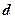на базисные орты 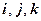соответственно (рис.2), а длина вектор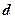а равна

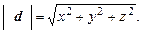
Date: 2015-04-23; view: 503; Нарушение авторских прав