Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Векторы. Линейные операции над векторами
|
|
Глава II
Векторная алгебра и аналитическая геометрия
Векторы. Линейные операции над векторами
Вектором называется направленный отрезок. Вектор, имеющий началом точку A, а концом точку B обозначают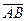 
или одной какой-нибудь буквой, например а, или 
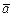. Модуль (длина) вектора обозначается 
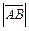, | а | или 
.
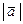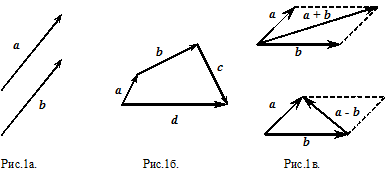
Векторы, параллельные одной прямой, называются коллинеарными. Векторы, параллельные одной плоскости, называются компланарными. Два вектора а и b (рис.1а) называются равными, если они имеют равные длины и сонаправлены.
Определим две основные операции векторной алгебры: умножение вектора на число и сложение векторов.
Произведением вектора а на число m называется новый вектор, имеющий длину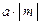 
и направленный одинаково с а (при 
) или противоположно а (при 
).
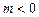Суммой векторов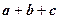 
называется вектор d (рис.1б), замыкающий ломаную, построенную из данных векторов. В частности, в параллелограмме, построенном на векторах a и b, одна вектор-диагональ есть сумма 
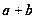, а другая есть разность 
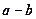данных векторов (рис.1в).
Date: 2015-04-23; view: 529; Нарушение авторских прав