Задание 7. Элементы аналитической геометрии на плоскости. Канонические уравнения линий второго порядка

Краткая теория. Уравнение линии на плоскости. Пусть на плоскости заданы декартова прямоугольная система координат и некоторая линия L. Рассмотрим уравнение 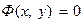(или 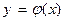), связывающее две переменные величины х и у. Это уравнение называется уравнением линии L (относительно заданной системы координат), если 1) ему удовлетворяют координаты 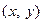любой точки линии L и 2) ему не удовлетворяют координаты ни одной точки, не лежащей на линии L.

Уравнение окружности. Пусть центр окружности радиуса R находится в точке 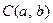, тогда для любой точки 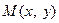, принадлежащей окружности, выполняется равенство 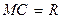или же 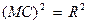, а для точек, не лежащих на окружности, это равенство выполняться не будет. Таким образом, уравнение рассматриваемой окружности имеет вид

.

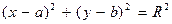В частности, уравнение 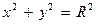является уравнением окружности радиуса R с центром в начале координат.

Часто используются так называемые параметрические уравнения окружности:

,

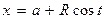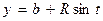
(для окружности с центром в начале координат эти уравнения принимают вид 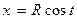, 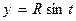). При изменении параметра t от 0 до 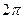точка (x (t), y (t)) опишет полную окружность.

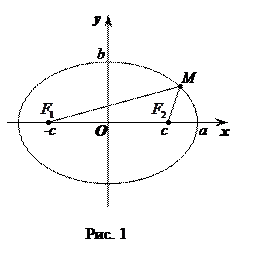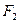Эллипсом называется линия, для каждой точки которой сумма расстояний до двух фиксированных точек и (фокусов) есть постоянная величина (обозначаемая 2 а).

В системе координат, изображенной на рис. 1, уравнение эллипса имеет простейший вид

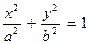, (1)

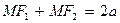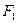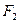называемый каноническим уравнением (оно получается из равенства ). Здесь а – большая полуось, b – малая полуось эллипса; фокусы и находятся на расстоянии 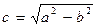от центра эллипса О (при этом предполагается, что 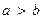). Отношение 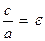называется эксцентриситетом эллипса (очевидно, 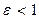); легко видеть, что 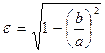. Расстояния от любой точки эллипса до его фокусов и 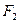(их называют фокальными радиусами-векторами) определяются по формулам

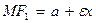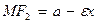, . (2)

Параметрические уравнения эллипса имеют вид

,

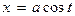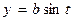
(при изменении параметра t от 0 до 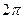точка (x (t), y (t)) описывает полный эллипс).

В случае, когда 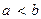, фокусы эллипса находятся на оси ординат; при этом , .

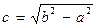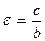Гиперболой называется линия, для каждой точки которой абсолютная величина разности расстояний до двух фиксированных точек 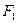и 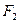(фокусов) есть постоянная величина (обозначаемая 2 а).

В системе координат, изображенной на рис. 2, уравнение гиперболы имеет простейший вид

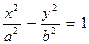, (4)

называемый каноническим уравнением (оно получается из равенства ).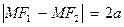

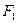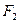Здесь а называется действительной полуосью, b – мнимой полуосью гиперболы; фокусы и находятся на расстоянии 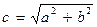от центра гиперболы О (при этом а может быть как больше, так и меньше b). Отношение 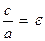называется эксцентриситетом гиперболы (очевидно, 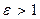); легко видеть, что .

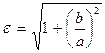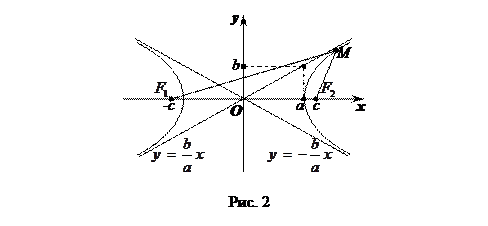
Прямые 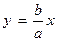и 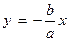называются асимптотами гиперболы; при неограниченном продвижении точки М (х, y) вдоль гиперболы в бесконечность расстояние от М до соответствующей асимптоты стремится к нулю.

Гипербола, у которой 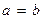, называется равнобочной; её уравнение 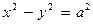. У равнобочной гиперболы асимптоты взаимно перпендикулярны, их уравнения 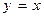и 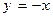; если взять эти асимптоты в качестве новых осей координат, то в такой системе координат х'Оу' уравнение такой гиперболы будет иметь вид 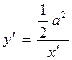, т.е. равнобочная гипербола в такой системе координат является графиком обратной пропорциональной зависимости.

Параболой называется линия, для каждой точки которой расстояние до фиксированной точки F (фокуса) равно расстоянию до данной прямой, называемой директрисой (прямая l на рис. 3).

Расстояние 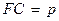от фокуса до директрисы называется параметром параболы. Принимая за начало координат середину О отрезка FC (так что 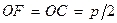) и располагая оси координат так, как показано на рис. 3, а, приходим к каноническому уравнению параболы: 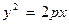(5)

(оно получается из равенства ).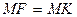

Парабола на рис. 3, а имеет фокус , а ее директриса описывается уравнением 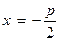. Расстояние от любой точки 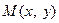параболы до ее фокуса (фокальный радиус-вектор) можно найти по формуле .

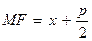Уравнение 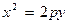представляет параболу, для которой ось симметрии совпадает с осью ординат, и парабола расположена так, как показано на рис. 5, б. Ее фокус 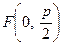, а директриса имеет уравнение .

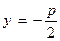Пример выполнения задания 7.Составить уравнение эллипса, симметричного относительно осей координат и проходящего через точк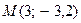и и .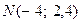

Решение. Подставляя координаты точек М и N в каноническое уравнение эллипса (1), получим систему двух уравнений для нахождения полуосей а и b:

, .

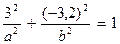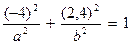Из этой системы находим 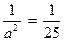, 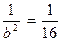(таким образом, большая полуось эллипса 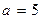, а малая полуось ).

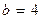Ответ: .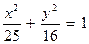

Date: 2015-04-23; view: 767; Нарушение авторских прав