Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задание 2. Умножение матриц
|
|
Даны квадратные матрицы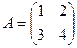 
и 
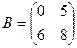. Найти два произведения AB и BA.
Воспользуемся правилами нелинейных операций:
1). Произведением матрицы А размером (m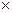 
n) и матрицы B размером (n 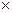l) называется матрица С размером (m l), в которой каждый элемент получен путем соответствующего перемножения и сложения элементов i -ой строки матрицы А и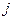 
столбца матрицы В:
; 
, 
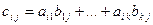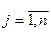
2). Транспонирование матриц — переход от матрицы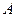 
к матрице 
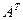, в которой строки и столбцы поменялись местами с сохранением порядка: строка №1 становится столбцом №1 и т.д.
Применим правило умножения. Сначала умножим A на B: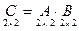 
= 
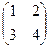
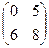
с11 = 1∙0 + 2∙6 = 12.
с12 = 1∙5 + 2∙8 = 21.
с21 = 3∙0 + 4∙6 = 24.
с22 = 3∙5 + 4∙8 = 47.
Получили: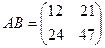 
.
Затем умножим B на A: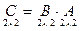 
=
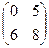
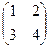
с11 = 0∙1 + 5∙3 = 15.
с12 = 0∙2 + 5∙4 = 20.
с21 = 6∙1 + 8∙3 = 30.
с22 = 6∙2 + 8∙4 = 44.
Получили: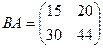 
.
Таким образом, A B ≠ B A.
Ответ: ; ;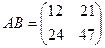 
.
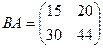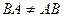Задание 3. Решение систем линейных алгебраических уравнений. Метод определителей. Матричный метод (с обратной матрицей). Метод исключения неизвестных Гаусса (с расширенной матрицей).
Найти решение системы линейных уравнений AX = B (где A – матрица коэффициентов при неизвестных данной системы уравнений, X – вектор неизвестных, B – столбец свободных членов):
а) систему AX = B1 решить методом определителей по формулам Крамера
для матрицы коэффициентов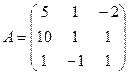 
; вектор-столбца неизвестных 
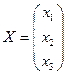; свободных членов 
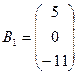. Система имеет вид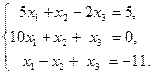 
Найдем главный определитель системы для матрицы А по правилу треугольников (правило Сарруса):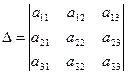 
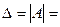a11 a22 a33 + a21 a32 a13 + a12 a23 a31 - a13 a22 a31 - a12 a21 a33 - a11 a23 a32
Это правило приведено на схеме с учетом знаков + и -:
(+) (-)
или на схеме
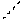
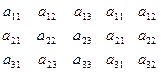
Вычислим определитель
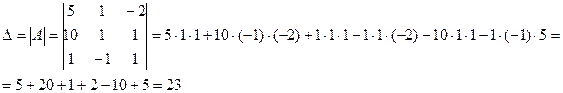
Так как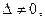 
то по теореме Крамера система имеет единственное решение.
Вычислим вспомогательные определители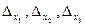 
, полученные из матрицы A, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
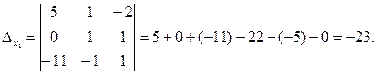
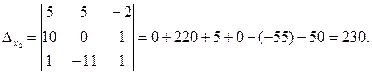
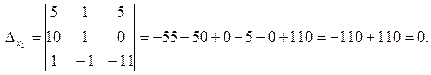
Теперь по формулам Крамера:
; 
; 
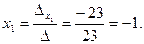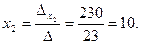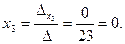
Таким образом неизвестные равны соответствующим значениям матрицы-строки или вектора (-1; 10; 0).
Сделаем проверку, подставив найденные значения в уравнения системы, и увидим, что они обратились в верные равенства:
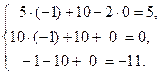или 
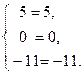(верно).
Ответ: вектор неизвестных (-1; 10; 0) или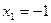 
, 
; 
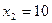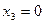
б) решить систему A X = B1 методом обратной матрицы. 
Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы матрица A была невырожденной, т. е. чтобы её определитель был отличен от нуля.
Запишем систему в виде матричного уравнения: A X = B 1, для
, , 
.
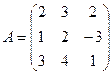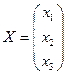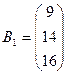Алгоритм решения матричного уравнения имеет вид:
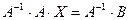
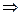
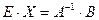
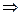
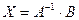
Чтобы получить вектор неизвестных, необходимо найти обратную матрицу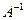 
.
Алгоритм получения обратной матрицы:
1. Находим определитель матрицы А.
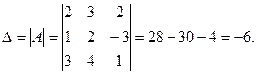
2. Транспонируем данную матрицу.
.
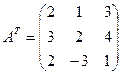3. Находим алгебраические дополнения транспонированной матрицы.
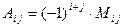вычеркиванием нужной строки № i и столбца № j с учетом знака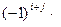 
,
, 
,
, 
, 
,
, 
, 
.
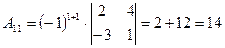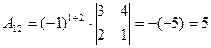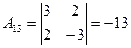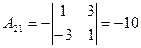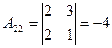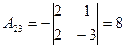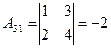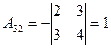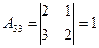4. Составим из них присоединенную матрицу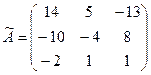 
5. Умножим присоединенную матрицу на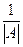 
, получим 
. 
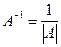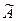
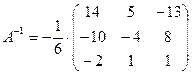- это обратная матрица.
6. Можно проверить, выполнив умножение А × А -1 – по определению обратной матрицы должна получиться единичная матрица Е:
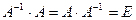
Для получения неизвестных, необходимо выполнить умножение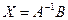 
:
.
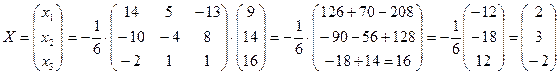Выполнив проверку, делаем вывод, что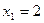 
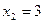
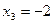так как
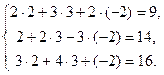
в) A X = B2 решить методом Гаусса;
Решим систему уравнений методом Гаусса для матриц коэффициентов, переменных и свободных членов:
, , 
.
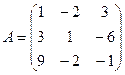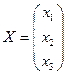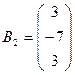Составим из них расширенную матрицу - сокращенную запись системы уравнений: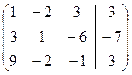 
.
Цель дальнейших действий – эквивалентными преобразованиями
строк (уравнений) привести расширенную матрицу к треугольному виду.
Так как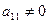 
, то умножим первую строку на (
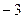) и прибавим ко второй строке, записывая сумму на месте второй строки:
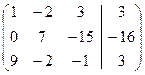
Умножим первую строку на (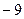
) и прибавим к третьей строке, записывая на месте третьей строки:
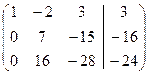. Таким образом, исключена переменная 
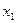из всех строк, начиная со второй.
Можно третью строку умножить на ¼: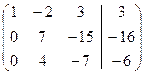 
Для исключения переменной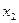 
из третьей строки, умножим вторую строку на 
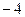, а третью строку на 7 и сложим, записывая результат на месте третьей строки:
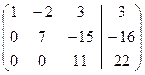
Прямой ход метода Гаусса закончен. Получена система уравнений:
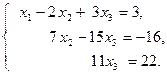
Используя обратный ход метода Гаусса, из третьего уравнения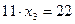 
найдем переменную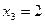 
.
Из второй строки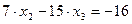 
выразим 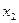подстановкой
значения 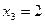. После вычислений получим 
.
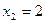Из первой строки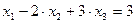 
выразим 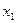через значения 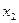и 
и 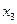получим 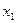=1. Таким образом, решение системы имеет вид (1; 2; 2).
Обычно делают проверку, подставив найденные значения в уравнения системы.
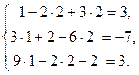или 
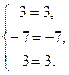(верно).
Ответ: (1; 2; 2) или 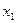=1, ,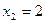
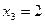
Date: 2015-04-23; view: 757; Нарушение авторских прав