Задание 5. Линейные векторные пространства. Базис. Координаты. Разложение векторов по базису

1) Выяснить, являются ли векторы

= (1, 3, 1), 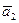= (2, 1, 1) и 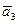=(3,—1,1) линейно зависимыми.

Решение. Составим векторное равенство

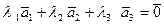или

.

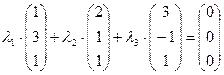Задача свелась, таким образом, к решению системы:

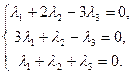
Решая систему методом Гаусса, приведем ее к виду:

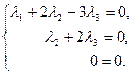
Откуда найдем бесконечное множество ее решений

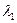( = с, 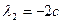, 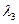= с), где с ─ произвольное действительное число.

Итак, для данных векторов условие линейной зависимости и независимости выполняется не только при 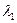= 0, 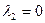, 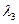= 0 (а, например, при 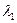= 1, 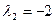, 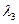= 1 (с = 1) и т.д.), следовательно, эти векторы — линейно зависимые и базиса не образуют.

Можно сделать важный вывод – определитель матрицы, составленной из координат линейно зависимых векторов равен нулю. Таким образом, чтобы проверить вектора на линейную зависимость или независимость, достаточно вычислить определитель матрицы, составленной из координат векторов и сравнить его с нулем

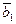б) В декартовом базисе заданы векторы = (1; 1; 0), 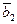= (1; —1; 1),

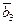= (- 3; 5; — 6) и .

Показать, что векторы 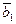, , 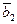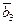- линейно независимы, то есть образуют базис и разложить вектор 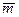по этому базису.

Решение.

Date: 2015-04-23; view: 581; Нарушение авторских прав