Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Методические указания к решению типовых заданий
|
|
Методические рекомендации
По выполнению контрольных работ
САМАРА
УДК – 517.2(07)
ЛИНЕЙНАЯ АЛГЕБРА. Методические рекомендации по выполнению контрольных работ. /Составители: Л.С. Клентак, Т.Д. Коваленко, В.Р. Каргин – Самара: МИР, 2013. – 32 с.
Методические указания содержат варианты контрольных заданий по дисциплине «Линейная алгебра» с элементами аналитической геометрии и примеры решения типовых задач.
Методические указания предназначены для студентов всех форм обучения Международного института рынка, обучающихся по направлениям подготовки с квалификацией бакалавр экономики, бакалавр прикладной информатики или бизнес информатики.
Составители: ст. преподаватель Клентак Людмила Стефановна
доцент Коваленко Татьяна Дмитриевна
Профессор Каргин Владимир Родионович
Рецензент: к.ф.-м.н. Тяпухина А.А.
Печатается по решению Научно-методического совета
Международного института рынка
© Международный институт рынка, 2013
СОДЕРЖАНИЕ
1. Тематическое содержание дисциплины……………………………….3
2. Варианты контрольной работы………………………………………...4
3. Методические указания к решению типовых заданий.
Краткая теория и примеры выполнения ………………………………15
4. Образцы тестовых заданий для промежуточного контроля………….28
Список литературы…………………………………………………………31
ТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
1. Основные алгебраические структуры.
Матрицы, действия над матрицами. Определители, их свойства. Разложение определителя по элементам строки или столбца. Понятие определителя n-го порядка. Определение и вычисление обратной матрицы.
2. Системы линейных уравнений в матричной записи.
Методы решения систем линейных уравнений: а) метод определителей - формулы Крамера; б) матричный метод (с помощью обратной матрицы коэффициентов); в) метод исключения неизвестных Гаусса (с эквивалентными преобразованиями расширенной матрицы. Однородные системы линейных уравнений.
3. Линейные (векторные) пространства.
Понятие n -мерного линейного векторного пространства. Понятие линейной зависимости/независимости системы векторов. Базис, координаты, размерность. Линейные преобразования пространств - линейные операторы. Матричная запись линейных операторов. Действия над линейными операторами и соответствующие действия над их матрицами. Собственные векторы и собственные значения. Понятие n - мерного евклидова пространства со скалярным произведением.
4. Элементы векторной алгебры на плоскости и в пространстве.
Векторная алгебра. Понятие вектора, длина вектора. Равенство векторов. Линейные операции над векторами. Декартов базис. Линейные операции над векторами, заданными координатами. Скалярное произведение векторов, свойства. Векторное произведение векторов, свойства. Смешанное произведение векторов, свойства.
5. Линии на плоскости.
Координаты на плоскости: декартовы, полярные. Уравнение прямой: с угловым коэффициентом, общее, в отрезках, проходящей через две данные точки. Угол между двумя прямыми, условия параллельности и перпендикулярности прямых.
Линии второго порядка. Канонические уравнения окружность эллипс, гипербола, парабола. Геометрический смысл параметров. Квадратичные формы.
6. Элементы аналитической геометрии в пространстве.
Плоскость: общее уравнение, понятие нормального вектора, частные случаи расположения в пространстве.
Прямая в пространстве: понятие направляющего вектора, каноническое уравнение прямой, общее уравнение, параметрические уравнения.
Взаимное положение прямых и плоскостей в пространстве. Условия параллельности и перпендикулярности объектов. Обзор поверхностей 2-го порядка.
ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ
Вариант №1
Задания:
1. Даны две матрицы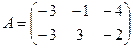 
и 
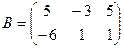. Найти матрицу 
.
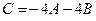2 а) Даны две квадратные матрицы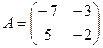 
и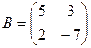 
. Найти произведения матриц AB и BA.
б) Найти произведение матриц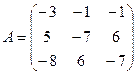 
и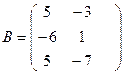 
.
3. Найти решение системы линейных уравнений АX = B1 для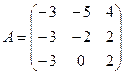 
– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
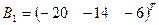– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX =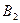 
методом Гаусса для , 
;
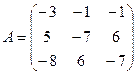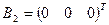5. Даны две системы векторов: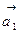 
(5,-1,4); 
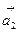(1,2, 3); 
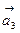(4,-2,1) и 
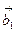(1,-1,2) 
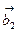(2, 1, 1), 
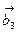(1, 4, 3).Определить, какая из этих систем образует базис; разложить вектор 
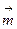(1, 4, 3) по этому базису.
6. Пользуясь уравнением Леонтьева (X=AX+Y),. найти конечный продукт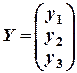 
для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 
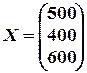и матрица коэффициентов прямых затрат 
.
7. Выяснить геометрический смысл уравнения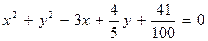 
. Записать каноническое уравнение, построить линию.
Вариант №2
Задания:
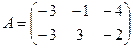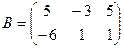1. Даны две матрицы и . Найти матрицу 
.
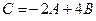2. а) Даны две квадратные матрицы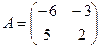 
и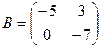 
. Найти произведения матриц AB и BA.
б) Для матриц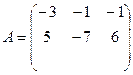 
и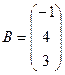 
найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для 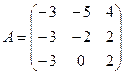– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
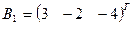– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = 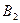методом Гаусса для 
, ;
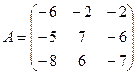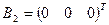5. Даны две системы векторов: 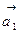(2,0,-1); 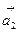(3,-5,4); 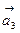(0,0,2) и 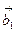(1,1,1);) 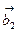((-2,3,0); 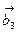(-3,7,1).Определить, какая из этих систем образует базис; разложить вектор 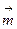(3, -5, 6) по этому базису.
6. Пользуясь уравнением Леонтьева (X=AX+Y),. найти конечный продукт 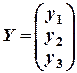для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 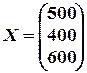и матрица коэффициентов прямых затрат 
.
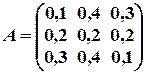7. Составить каноническое уравнение гиперболы, проходящей через точк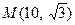и 
и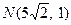 
. Сделать геометрическую иллюстрацию.
Вариант №3
Задания:
1. Даны две матрицы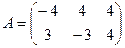 
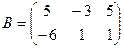и . Найти матрицу 
.
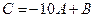2. а) Даны две квадратные матрицы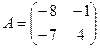 
и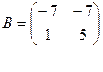 
. Найти два произведения матриц AB и BA.
б) Для матриц 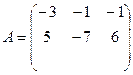и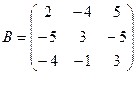 
найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для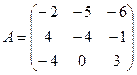 
– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
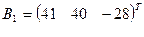– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = 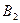методом Гаусса для 
, ;
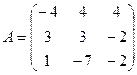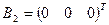5. Даны две системы векторов: 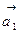, , 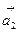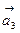и 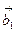, , 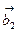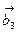.Определить, какая из этих систем образует базис; разложить вектор 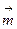по этому базису.
|
|
|
|
|
|
| ||
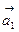
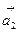
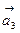
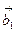
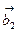
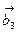
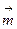
| (4,0,-2) | (3,-5,4) | (0,0,2) | (2,2,2) | (-2,3,0) | (-3,7,1) | (3,-5,6) |
6. Пользуясь уравнением Леонтьева (X=AX+Y),. найти конечный продукт 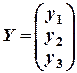для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 
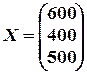и матрица коэффициентов прямых затрат .
7. Составить каноническое уравнение параболы, проходящей через точк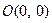и 
и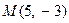 
, симметричной относительно оси абсцисс. Сделать геометрическую иллюстрацию.
Вариант №4
Задания:
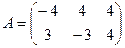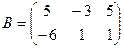1. Даны две матрицы и . Найти матрицу 
.
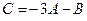2. а) Даны две квадратные матрицы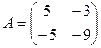 
и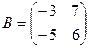 
. Найти два произведения матриц AB и BA.
б) Для матриц 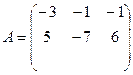и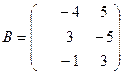 
найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для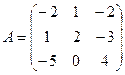 
– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
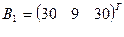– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = 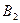методом Гаусса для 
, ;
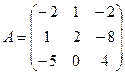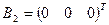5. Даны две системы векторов: 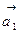, , 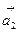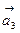и 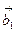, , 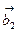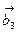.Определить, какая из этих систем образует базис; разложить вектор 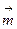по этому базису.
| № вар |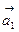
|
|
|
|
|
|
|
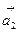
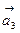
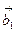
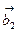
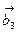
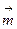
| (-1,1,3) | (1,3,1) | (2,-1,-1) | (-3,1,-1) | (1,-1,1) | (-1,-1,1) | (-3,5,8) |
6. Пользуясь уравнением Леонтьева (X=AX+Y), найти конечный продукт 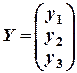для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 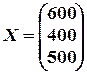и матрица коэффициентов прямых затрат .
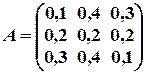7. Составить уравнение эллипса, симметричного относительно осей координат и проходящего через точк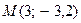и 
и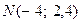 
. Сделать графическую иллюстрацию.
Вариант №5
Задания:
1. Даны две матрицы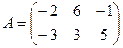 
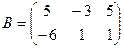и . Найти матрицу 
.
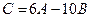2. а) Даны две квадратные матрицы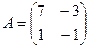 
и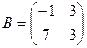 
. Найти два произведения матриц AB и BA.
б) Для матриц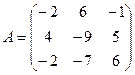 
и 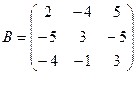найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для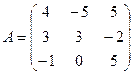 
– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
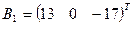– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = 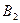методом Гаусса. Здесь 
, ;
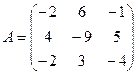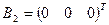5. Даны две системы векторов: 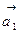, , 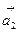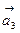и 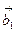, , 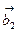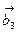.Определить, какая из этих систем образует базис; разложить вектор 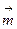по этому базису.
| № вар |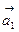
|
|
|
|
|
|
|
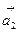
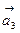
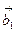
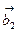
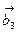
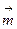
| (-5,7,4) | (1,3,1) | (2,-1,-1) | (5,2,3) | (1,0,5) | (2,1,-1) | (0,8,3) |
6. Пользуясь уравнением Леонтьева (X=AX+Y), найти конечный продукт 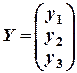для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 
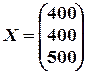и матрица коэффициентов прямых затрат .
7. Составить каноническое уравнение гиперболы, проходящей через точк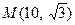и и 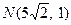. Сделать геометрическую иллюстрацию.
Вариант №6
Задания:
1. Даны две матрицы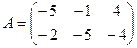 
и 
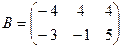. Найти матрицу 
.
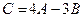2. а) Даны две квадратные матрицы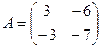 
и 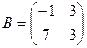. Найти два произведения матриц AB и BA.
б) Для матриц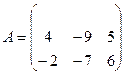 
и 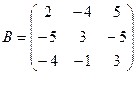найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для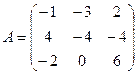 
– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
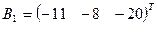– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = методом Гаусса для 
, ;
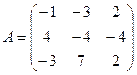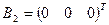5. Даны две системы векторов: 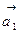, , 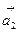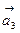и 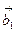, , 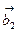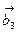.Определить, какая из этих систем образует базис; разложить вектор 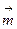по этому базису.
| № вар |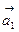
|
|
|
|
|
|
|
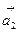
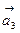
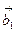
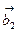
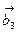
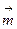
| (1,0,1) | (-1,1,2) | (3,5,1) | (2,-1,3) | (1,1,-4) | (4,1,-5) | (2,1,-2) |
6. Пользуясь уравнением Леонтьева (X=AX+Y), найти конечный продукт 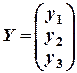для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 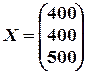и матрица коэффициентов прямых затрат .
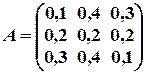7. Выяснить геометрический смысл уравнения 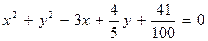. Записать каноническое уравнение, построить линию.
Вариант №7
Задания:
1. Даны две матрицы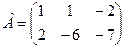 
и 
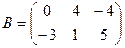. Найти матрицу 
.
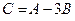2. а) Даны две квадратные матрицы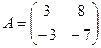 
и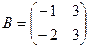 
. Найти два произведения матриц AB и BA.
б) Для матриц 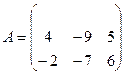и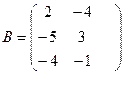 
найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для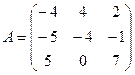 
– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
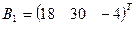– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = 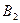методом Гаусса для 
, ;
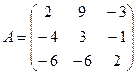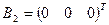5. Даны две системы векторов: 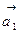, , 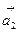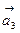и 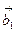, , 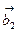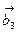.Определить, какая из этих систем образует базис; разложить вектор 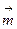по этому базису.
| № вар |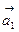
|
|
|
|
|
|
|
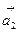
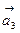
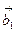
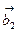
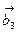
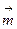
| (2,1,3) | (-1,0,1) | (0,1,-1) | (2,-2,1) | (-1,0,1) | (-1,-2,4) | (5,3,10) |
6. Пользуясь уравнением Леонтьева (X=AX+Y),. найти конечный продукт 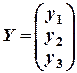для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 
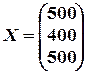и матрица коэффициентов прямых затрат .
7. Составить каноническое уравнение параболы, проходящей через точк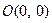и и 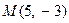и симметричной относительно оси абсцисс. Сделать геометрическую иллюстрацию
Вариант №8
Задания:
1. Даны две матрицы 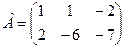и 
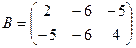. Найти матрицу 
.
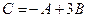2. а) Даны квадратные матрицы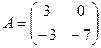 
и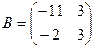 
. Найти два произведения матриц AB и BA.
б) Для матриц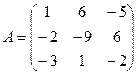 
и 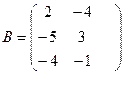найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для
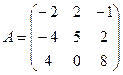– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
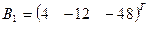– столбца свободных членов а) методом определителей по формулам Крамера; б) методом обратной матрицы.
4. Решить однородную систему AX = 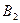методом Гаусса для 
, ;
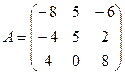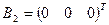5. Даны две системы векторов: 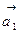, , 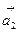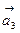и 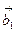, , 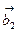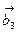.Определить, какая из этих систем образует базис; разложить вектор 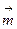по этому базису.
| № вар |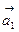
|
|
|
|
|
|
|
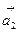
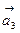
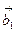
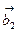
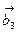
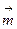
| (1,-2,1) | (3,4,-1) | (2,6,2) | (2,2,3) | (1,2,3) | (1,1,1) | (3,0,-2) |
6. Пользуясь уравнением Леонтьева (X=AX+Y),. найти конечный продукт 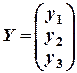для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 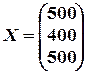и матрица коэффициентов прямых затрат .
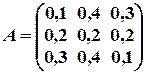7. Составить уравнение эллипса, симметричного относительно осей координат и проходящего через точк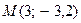и и 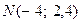. Сделать графическую иллюстрацию.
Вариант №9
Задания:
1. Даны две матрицы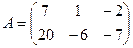 
и 
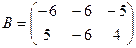. Найти матрицу 
.
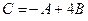2. а) Даны квадратные матрицы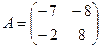 
и 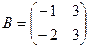. Найти два произведения матриц AB и BA.
б) Для матриц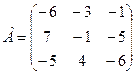 
и 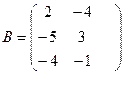найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для
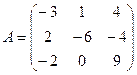– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
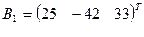– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = 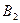методом Гаусса для 
, .
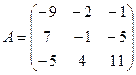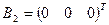5. Даны две системы векторов: 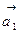, , 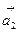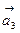и 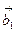, , 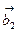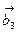.Определить, какая из этих систем образует базис; разложить вектор 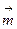по этому базису.
| № вар |
|
|
|
|
|
|
|
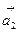
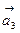
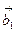
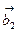
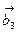
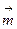
| (4,-2,3) | (1,-3,1) | (-3,-1,-2) | (1,1,1) | (0,1,1) | (0,0,1) | (5,6.-3) |
6. Пользуясь уравнением Леонтьева (X=AX+Y),. найти конечный продукт 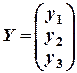для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 
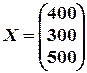и матрица коэффициентов прямых затрат .
7. Составить каноническое уравнение гиперболы, проходящей через точк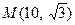и и 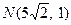. Сделать геометрическую иллюстрацию.
Вариант №10
Задания:
1. Даны две матрицы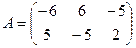 
и 
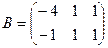. Найти матрицу 
.
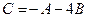2. а) Даны квадратные матрицы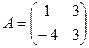 
и 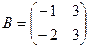. Найти два произведения матриц AB и BA.
б) Для матриц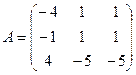 
и 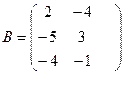найти произведение AB.
3. Найти решение системы линейных уравнений АX = B1 для
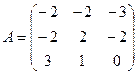– матрицы коэффициентов при неизвестных системы линейных уравнений, X – вектора-столбца неизвестных; 
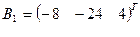– столбца свободных членов
а) методом определителей по формулам Крамера;
б) методом обратной матрицы.
4. Решить однородную систему AX = 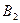методом Гаусса для 
, ;
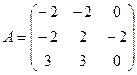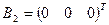5. Даны две системы векторов: 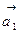, , 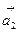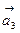и 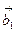, , 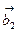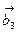.Определить, какая из этих систем образует базис; разложить вектор 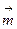по этому базису.
| № вар |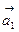
|
|
|
|
|
|
|
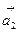
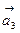
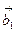
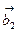
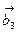
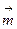
| (4,2,3) | (1,-3,1) | (-2,0,2) | (4,-1,3) | (1,1,-2) | (7,2,-3) | (3,2,-1) |
6. Пользуясь уравнением Леонтьева (X=AX+Y),. найти конечный продукт 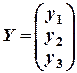для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли 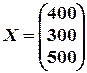и матрица коэффициентов прямых затрат .
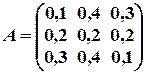7. Выяснить геометрический смысл уравнения 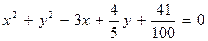. Записать каноническое уравнение, построить линию.
Методические указания к решению типовых заданий.
Date: 2015-04-23; view: 969; Нарушение авторских прав