Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задание 4. Однородные системы линейных уравнений
|
|
A X = 0 - решить однородную систему методом Гаусса;
Решим систему уравнений методом Гаусса для заданных матриц
коэффициентов, переменных и нулевых свободных членов:
, 
, 
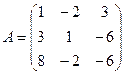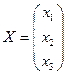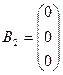. исправить
Составим расширенную матрицу - сокращенную запись системы уравнений: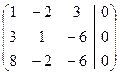 
.
Приведем расширенную матрицу к треугольному виду при помощи эквивалентных преобразований строк (уравнений):
Так как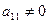 
, то умножим первую строку на (
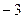) и прибавим ко второй строке, записывая сумму на месте второй строки:
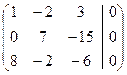
Умножим первую строку на (-8) и прибавим к третьей строке, записывая на месте третьей строки:
.
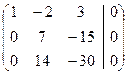Таким образом, исключена переменная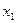 
из всех строк, начиная со второй.
Третью строку можно умножить на (-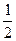 
) и сложить со второй,
записав результат на место третьей строки:
.
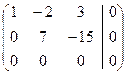Эта расширенная матрица равносильна преобразованной системе
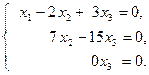
Система имеет решение для любых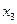 
. обозначим это 
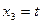любое число.
Выразим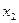 
из второй строки 
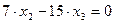через :
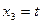и после вычислений получим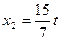 
.
Из первого уравнения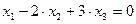 
выразим через t переменную
= 
.
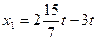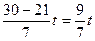Таким образом, существует бесчисленное множество наборов решений данной однородной системы в виде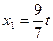 
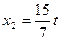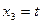, , , где t – любое число.
Date: 2015-04-23; view: 529; Нарушение авторских прав