Первый способ решения

Векторы 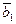, , 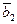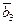образуют базис, если они линейно независимы. Составим векторное равенство: 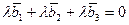. Решая соответствующую ему однородную систему, можно убедиться в единственном нулевом решении: 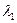= 0, 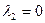, 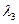= 0. То есть векторы 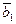, , 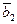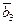дают линейную нулевую комбинацию только при одновременном равенстве нулю коэффициентов – значит они образуют систему линейно независимых векторов и, следовательно, составляют базис.

Запишем разложение векторов 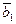, , 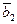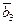в начальном заданном базисе (координаты вектора в базисе – это коэффициенты его разложения по базисным векторам):

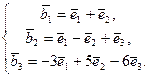
Матрица перехода от базиса к базису 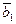, , 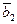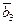имеет вид

.

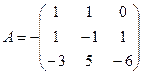После вычисления обратной матрицы

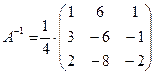
и ее транспонирования

.

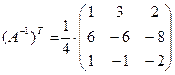можно записать формулы перехода к новому базису в матричной форме:

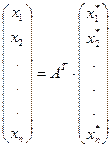или .

Итак имеем:

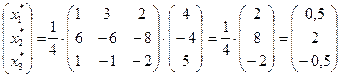, т.е. новые координаты вектора 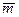в базисе 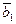, , 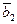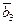есть 0,5; 2 и -0,5 и вектор 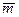может быть представлен в виде линейной комбинации:

.

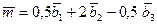Второй способ решения:

Проведем разложение вектора по базису , , .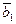

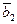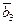Запишем разложение вектора 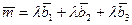в координатной форме:

.

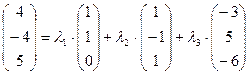Получаем систему линейных уравнений относительно коэффициентов разложения в новом базисе , , :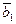

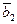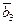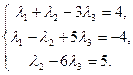
Систему можно решать любым способом. Решим по формулам Крамера. Вычислим определители:

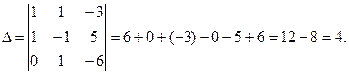
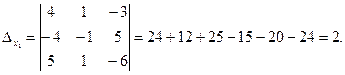
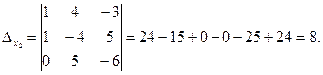
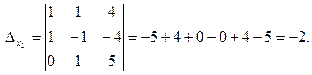
Теперь по формулам Крамера:

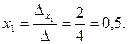
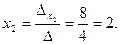
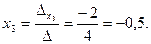
Т.е. решение системы (0,5; 2; -0,5).

Новые координаты вектора 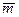в базисе 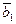, , 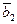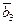есть 0,5; 2 и -0,5 и вектор 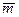может быть представлен в виде:

.

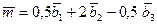Задание 6. Применение матриц в экономике. Пользуясь уравнением Леонтьева, X=AX+Y найти конечный продукт Y для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли X и матрица коэффициентов прямых затрат A. Решить при ; .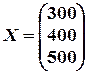

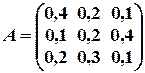Решение

Из уравнения Леонтьева X=AX+Y определяем Y по формуле:
Y = X – AX.

= – × =

= – = .

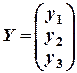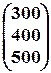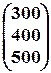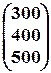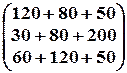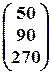Таким образом, y ₁ = 50, y ₂ = 90, y ₃ = 270.

Date: 2015-04-23; view: 728; Нарушение авторских прав