Лабораторна робота 7

Розрахунок інформаційних ланцюгів

Теоретичні відомості. Інформаційний ланцюг являє собою сукупність взаємодіючих джерел, перетворювачів і споживачів інформації. Інформаційні ланцюги можуть розглядатися як моделі процесів у системах керування різної природи. У загальному випадку інформаційні ланцюги являють собою досить складні сильно розгалужені структури. У найпростішому випадку система керування може бути представлена інформаційним ланцюгом, що містить джерело, приймач і два інформаційних канали (рис. 1).

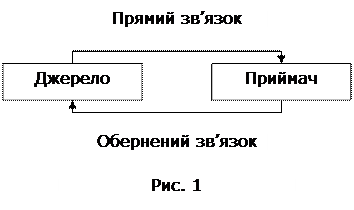При цьому керуючий пристрій виступає в ролі джерела керуючої інформації, а керований об'єкт – у ролі приймача чи інформаційного навантаження. Формалізація інформаційних ланцюгів може бути виконана з використанням типових ідеалізованих елементів за аналогією з електричними, механічними, пневматичними ланцюгами.

Інформаційна напруга джерела дорівнює різниці ентропій об'єкта керування (чи логарифму відношення ймовірностей) без керування Н₀ і при наявності керування Н₁, тобто

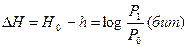. (1)

Інформаційний опір приймача дорівнює часу реакції об'єкта керування на керуючу інформацію r_Н (с).

Інформаційний струм через активне навантаження дорівнює відношенню

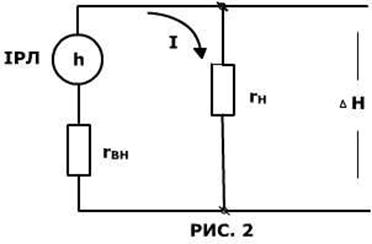
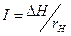(біт/с). (2)

Джерело інформації також характеризується опором r_вн, що визначається часом прийняття рішення. Крім внутрішнього опору r_вн джерело характеризується величиною информаційно-рухівної логіки ІРЛ h, рівний інформаційній напрузі на холостому ходу. ІРЛ характеризує інтелектуальні можливості джерела при необмеженому часі на прийняття рішень. Таким чином найпростіший повний інформаційний ланцюг має наступну структуру (рис. 2).

Для цієї схеми інформаційний струм дорівнює

.

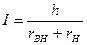Крім того

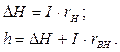
У загальному випадку навантаження характеризується крім інформаційного опору також пам'яттю і ригідністю.

Пам'ять визначається ємністю n, що дорівнює відношенню запом’ятованої інформації 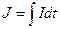до її потенціалу (напрузі) 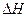, тобто

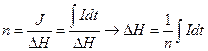. (3)

Ригідністю називається властивість навантаження, що виражається в активній протидії керуванню, тобто у виробленні навантаженням зустрічної інформаційної напруги

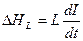; (4)

,

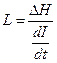де L – ригідність (з²).

З урахуванням властивостей пам'яті і ригідності інформаційні ланцюги можуть мати більш складну структуру. Для розрахунку таких ланцюгів використовуються універсальні формули, що виражають закони Кірхгофа для інформаційних ланцюгів.

1. Для будь-якого вузла інформаційного ланцюга алгебраїчна сума струмів дорівнює нулю

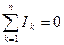. (5)

2. Сума падінь напруг уздовж будь-якого замкнутого контуру інформаційного ланцюга дорівнює нулю

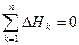. (6)

За відомими струмами і напругами можливо розрахувати інформаційну потужність

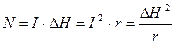. (7)

Інформаційна потужність трактується як зміст, що розсіюється (на навантаженні) чи виробляється (джерелом) за одиницю часу. Із відповідної інтелектуальної діяльності

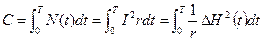. (8)

Якщо інформаційний ланцюг містить джерела і тільки активні елементи r, то ви0рази (5), (6) являють собою систему алгебраїчних рівнянь.

Приклад 1. Інформаційний ланцюг заданий структурною схемою (рис. 3). Потрібно розрахувати інформаційні струми в ланцюзі, а також зміст С₄, розсіяний на елементі r₄ за дві години роботи системи, якщо h=10 біт; r_вн=0.5 с; r₁=1 c; r₂=r₃=5 c; r₄=2 c.

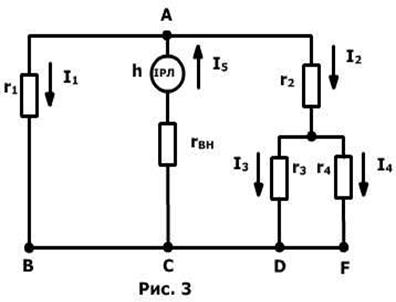Використовуючи співвідношення (5) і (6) складемо 5 алгебраїчних рівнянь для визначення інформаційних струмів I₁, I₂, I₃, I₄, I_5.

I₅=I₁+I₂ – для вузла А

I₂=I₃+I₄ – для вузла Е

h=I₅r_BH+I₁r₁ – для контуру ABC

h=I₂r₂+I₃r₃ – для контуру AEDC

I₃r₃=I₄r₄ – для контуру DEF.

Підставляючи значення параметрів, отримаємо

.

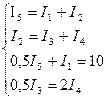Розв’язуючи систему, знайдемо: I₁=2,963 біт/з; I₂=11,111 біт/з; I₃=8,889 біт/с; I₄=2,222 біт/с; I₅=14,074 біт/с.

Потужність, що розсіюється на елементі r₄, дорівнює

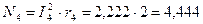біт/с.

Враховуючи те, що n₄ не залежить від часу, визначимо зміст, розсіяний на r₄ за другу годину роботи

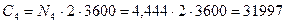біт².

Якщо інформаційний ланцюг містить запам'ятовуючі і ригідні елементи, то вирази (5), (6) являють собою систему диференціальних рівнянь, що описує перехідні процеси в ланцюзі для заданих значень параметрів і початкових умов. При цьому струми, напруги і потужності будуть являти собою функції часу.

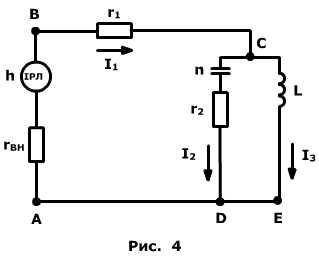Приклад 2. Інформаційний ланцюг заданий структурною схемою (рис. 4). Для заданих значень параметрів і початкових умов потрібно визначити закон зміни інформаційного струму на елементі r₂, а також зміст, розсіяний на цьому елементі за інтервал часу 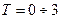c.

r_BH=1 c; r₁=0,6 c; r₂=2 c; n=2; L=0,5 c²; h=1 біт; .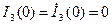

Відповідно до співвідношень (5), (6), складемо систему диференціальних і алгебраїчних рівнянь для визначення інформаційних струмів у ланцюзі

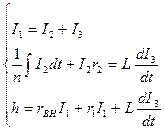
- для вузла С;

- для контуру DCE;

- для контуру ABCE.

Уведемо позначення r_BH+r₁=2. Тоді з врахуванням того, що I₁=I₂+I₃, третє рівняння системи прийме вигляд:

.

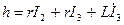Друге рівняння перепишемо так

.

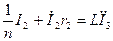Маємо систему

.

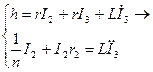
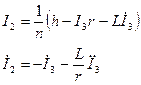Поставимо у вирази для 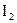і 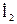в друге рівняння системи і приведемо подібні

.

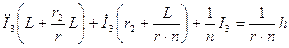З врахуванням відомих вихідних даних

.

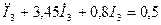Розв’язок рівняння знаходиться у вигляді суми

,

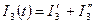де I”₃ – розв’язок алгебраїчного рівняння

.

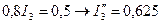I’₃ є розв’язок вихідного диференціального рівняння без правої частини

.

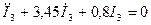Таким чином, корені характеристичного рівняння

.

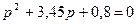дійсні р₁=-0,25; р₂=-3,2, і рішення для I’₃ є сума експонент

.

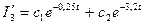Виходить, загальний розв’язок має вигляд

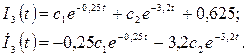
Постійні с₁ і с₂ знайдемо з урахуванням початкових умов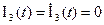

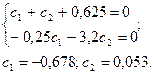
Частинний розв’язок для I₃ має вигляд

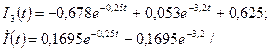
Закон зміни інформаційного струму I₂

.

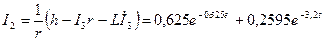Процес зміни інформаційної потужності на опорі r₂

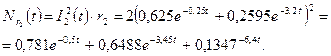
Зміст, розсіяний на елементі r₂ за інтервал часу 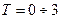c дорівнює

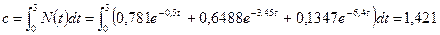біт.

Завдання. Для заданого інформаційного ланцюга розрахувати інформаційні струми, потужність і зміст, що розсіюються на виділеному елементі.

ЗМІСТ

Вступ................................................................................................................ 3

Лабораторна робота 1 “Структурно-топологічний аналіз систем”........................4

Лабораторна робота 2 «Аналіз систем із застосуванням марковських процесів.”......................................................................................................................... 15

Лабораторна робота 3 “Дослідження систем керування за допомогою імітаційного моделювання.”................................................................................................ 19

Лабораторна робота 4 ” Розрахунок характеристик моделей масового обслуговування.”......................................................................................................................... 26

Лабораторна робота 5… “Визначення кількості інформації в незалежних повідомленнях.”.............................................................................................. 31

Лабораторна робота 6 Інформаційний аналіз залежних повідомлень....... 38

Лабораторна робота 7. Розрахунок інформаційних ланцюгів................... 43

Укладачі:

Ігор Валерійович Новицький

Микола Миколайович Одновол

Date: 2015-05-22; view: 566; Нарушение авторских прав