
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторна робота 2
|
|
Аналіз систем із застосуванням марковських процесів
Апарат марковських випадкових процесів широко використовується при аналізі складних систем керування для опису їхнього поводження при наявності випадкових факторів.
Маємо випадковий процес, що протікає в системі з можливими станами Z0,Z1,...Zi,...Zj.. Позначимо умовну ймовірність того, що в момент t =t0+T система перейде у стан Zj, якщо в момент t0 вона знаходилась у стані Zi через Pij(t0,Т). Дискретний випадковий процес називається марковським, якщо ймовірність Ріj(t0,Т) залежить тільки від і, j, t0, T, тобто тільки від того, у якому стані система була у момент t0 і в який стан вона перейде через час Т.
Марковським процесом з неперервним часом називається процес, у якого перехід з одного стану в інший можливий у будь-який момент часу. Такий клас процесів широко використовується для аналізу поводження складних систем керування.
Для опису поводження системи в класі марковських процесів з неперервним часом необхідно:
1) Увести поняття стану системи.
2) Указати всі стани, у яких може знаходитися система.
3) Скласти граф станів, тобто вказати шляхи можливих безпосередніх переходів системи зі стану в стан.
4) Для розрахунку перехідних процесів у системі вказати, у якому стані знаходиться система в початковий момент часу.
5) Для кожного можливого переходу на графі вказати інтенсивність 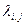 потоку подій, що переводять систему зі стану Zi у стан Zj. Звичайно інтенсивності
потоку подій, що переводять систему зі стану Zi у стан Zj. Звичайно інтенсивності 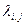 визначаються експериментально.
визначаються експериментально.
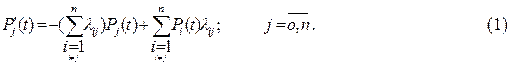 |
Вичерпною характеристикою марковського процесу є сукупність імовірностей Pj(t) того, що процес у момент часу t буде знаходитися в стані Zj
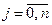 . Ці ймовірності визначаються на основі розв'язку диференціальних рівнянь
. Ці ймовірності визначаються на основі розв'язку диференціальних рівнянь
Система (1) визначає перехідний процес у припущенні, що початковий стан –P0.
Якщо число станів системи n - кінцеве і з кожного стану графа можливо перейти в будь-який інший стан, то така система буде мати граничний стаціонарний режим. Так, система (рис.1а) має стаціонарний режим, а система (рис. 1б) – не має.

Рис. 1, а Рис. 1, б
З практичної точки зору має інтерес визначення ймовірностей станів системи в граничному стаціонарному режимі.
Для їхнього розрахунку використовується система алгебраїчних рівнянь, що виходить з (1) шляхом прирівнювання до нуля похідних
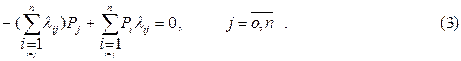 |
 |
Система (3) є лінійно залежною, тому її варто доповнити умовою
Приклад. Два абоненти А і В працюють з одним інформаційним центром. У визначений момент часу центр може обслуговувати тільки одного абонента. Абонент А має більш високий пріоритет, тому, якщо від А приходить заявка, обслуговування В припиняється до закінчення обслуговування А.
1. Розрахувати ймовірності можливих станів даної системи, якщо відомі інтенсивності потоків подій, що переводять систему в сусідні стани.
2. З'ясувати, чи буде система працювати ефективно, якщо для цього необхідно, щоб витрати часу абонента В на чекання склали б не більш 50% часу його обслуговування.
3. Установити які параметри і яким чином повинні змінитися, щоб підвищилася ефективність обслуговування абонента В?
Уведемо поняття стану системи. Стан системи визначається станом абонентів А і В. Для абонента А можливі два стани: 0 – відсутність заявки; 1 – обслуговування. Для абонента В можливі три стани: 0 – відсутність заявки; 1 – обслуговування; 2 – чекання обслуговування.
Тоді стани системи такі:
(0,0) – 1 – відсутність заявок від А і В;
(0,1) – 2 – відсутність заявки від А і обслуговування В;
(1,0) – 3 – обслуговування А і відсутність заявки від В;
(1,2) – 4 – обслуговування А і чекання обслуговування для В.
Граф стану системи має вигляд:
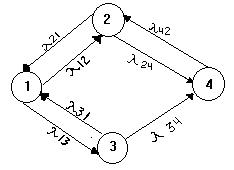
Рис.2
Відповідно до (3) складемо систему алгебраїчних рівнянь для визначення ймовірностей станів Pi i= 1,4:
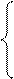
–(l12+l13)Р1+l21Р2+l31Р3=0
–(l21+l24)Р2+ l42Р4+l12Р1=0. (5)
–(l31+l34)Р3+l13Р1=0
–l42Р4+l24Р2+l34 Р3=0
Систему рівнянь можливо скласти безпосередньо за графом (рис.2), користаючись правилом: для кожного i-го стану складається одне рівняння, причому інтенсивності l, що беруться зі знаком мінус і перемножуються на Pi; інтенсивності, що входять в і перемножуються зі знаком плюс на ймовірності тих станів, з яких вони виходять.
Допустимі інтенсивності для графа (рис.2) задані і рівні: 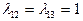 ;
; 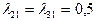 ;
; 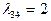 ;
; 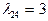 ;
; 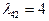 . Тоді система (5) прийме вигляд
. Тоді система (5) прийме вигляд 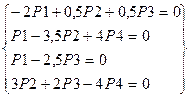 .
.
Отримана система є системою лінійно залежних рівнянь. По цьому одне рівняння (неважливо яке) системи необхідно замінити умовою (4)
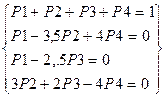 . (6)
. (6)
Розв'язуючи систему (6), наприклад, методом Гаусса, одержимо
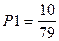 ;
; 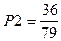 ;
; 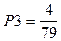 ;
; 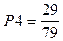 .
.
Відношення часу чекання і часу обслуговування абонента В визначається відношенням імовірностей станів Р4 і Р2
 .
.
Так як це відношення більше 0,5 (50%), то можна зробити висновок про неефективність роботи системи.
Щоб зменшити відношення 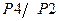 необхідно зменшити інтенсивність потоків
необхідно зменшити інтенсивність потоків 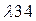 і
і 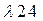 чи збільшити інтенсивність потоків
чи збільшити інтенсивність потоків 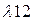 і
і 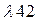 .
.
Завдання.1. Для заданого графа станів системи і інтенсивностей переходів розрахувати ймовірності станів системи.
Для виділених на графі ймовірності 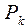 і інтенсивності
і інтенсивності 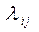 визначити, які значення повинні приймати інтенсивність
визначити, які значення повинні приймати інтенсивність 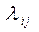 , щоб імовірність
, щоб імовірність 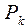 не перевищувала величину а(а - задане).
не перевищувала величину а(а - задане).
Завдання.2.* Скласти граф станів системи аналогічної приведеній у прикладі, але з трьома абонентами А, В, С, пріоритети яких мають вигляд
А>В>С.
Date: 2015-05-22; view: 606; Нарушение авторских прав