Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Лабораторна робота 6
|
|
Інформаційний аналіз залежних повідомлень
1. Короткі теоретичні відомості. При розв’язанні задач інформаційного аналізу часто доходиться досліджувати кілька джерел, що дають залежні повідомлення. Сукупність повідомлень, що виробляються декількома джерелами, називається складним повідомленням.
Маємо два джерела повідомлень. Події першого джерела приймають значення х1, х2,..., хn з імовірностями р(х1), р(х2),..., р(хn), а другого - y1, y2,..., ym з імовірностями р(y1),р(y2),..., р(ym). Спільна ентропія такого складного повідомлення визначається за формулою:
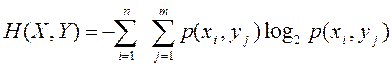, (1)
де p(xi,yi)- імовірність спільної появи повідомлень xi і yi. Для складних повідомлень мають місце співвідношення
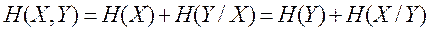, (2)
де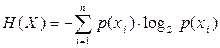 
- ентропія повідомлення х; (3)
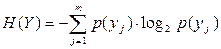- ентропія повідомлення у; (4)
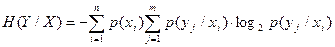- середня умовна ентропія повідомлення y(ентропія y за умови, що повідомлення x уже надійшло) (5);
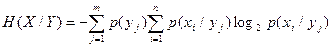- середня умовна ентропія повідомлення x (ентропія x за умови, що повідомлення y уже надійшло). (6)
На практиці при інформаційному аналізі складних повідомлень імовірності p(x), p(y), p(x/y), p(y/x) приблизно оцінюються відносними частотами, що обчислюються на основі експериментальних даних.
2. Постановка задачі. Для оцінки стану об'єкта використовуються два статистично залежних параметри X і Y.У результаті експерименту отримані реалізації процесів X(t), Y(t) на інтервалі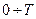 
. Потрібно виконати інформаційний аналіз складного повідомлення (X,Y) про стан об'єкта.
3. Методика рішення задачі.
3.1. Реалізації неперервних процесів X(t), Y(t) представляються у вигляді дискретних відліків Xk, Yk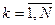 
(N- загальна кількість точок реалізації). Діапазони зміни X і Y розбиваються на n і m інтервалів у залежності від необхідної точності виміру 
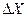і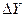 
.
3.2. Визначаються відносні частоти влучення X і Y в інтервали W(xi), W(yi), а також відносні частоти подій W(xi,yi). Складається таблиця.
| Yi | Xi | W(yj) | |||
| X1 | x2 | … | xn | ||
| y1 | W(x1, y1) | W(x2, y1) | … | W(xn, y1) | W(y1) |
| y2 | W(x1, y2) | W(x2, y2) | … | W(xn, y2) | W(y2) |
| … | … | … | … | … | … |
| ym | W(x1, ym) | W(x2, ym) | … | W(xn, ym) | W(ym) |
| W(xi) | W(x1) | W(x2) | … | W(xn) |
3.3. Оцінюється ентропія повідомлень H(x), H(Y), за формулами:
;
.
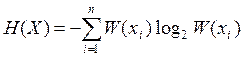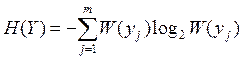3.4. Визначається ентропія складного повідомлення
.
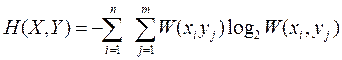3.5. Розраховується умовна ентропія по формулами:
;
.
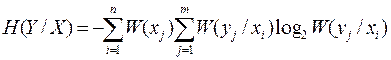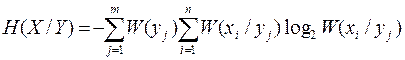3.6. Виконується перевірка розрахунків з використанням співвідношення
.
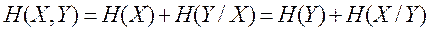4. Приклад. Вихідні дані. Дано дві реалізації процесів зміни статистично залежних параметрів X(t), Y(t).Потрібно виконати інформаційний аналіз складного повідомлення (X,Y). Крок квантування за часом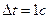 
. Необхідна точність виміру параметрів 
.
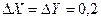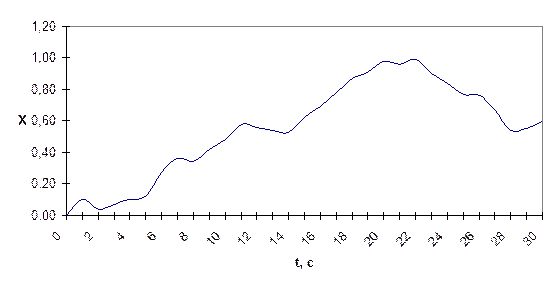
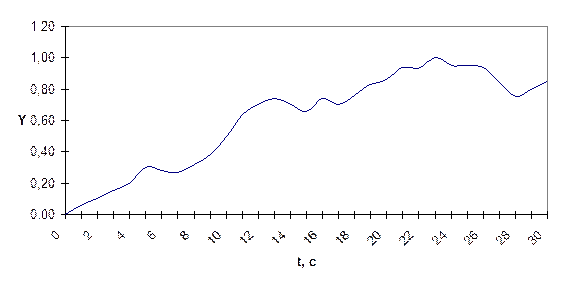
1.Неперервні реалізації X(t), Y(t) на інтервалі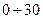 
c представляємо у вигляді дискретних відліків Xk, Yk 
, .
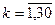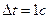Таблиця1
| T | |||||||||||||||
| X | 0.4 | 0.7 | 1.2 | 2.7 | 3.6 | 3.4 | 4.2 | 4.8 | 5.8 | 5.6 | 5.4 | 5.3 | 6.2 | ||
| Y | 0.6 | 1.5 | 2.8 | 2.7 | 3.2 | 3.8 | 6.4 | 7.4 | 6.6 |
| T | |||||||||||||||
| X | 6.9 | 7.8 | 8.7 | 9.1 | 9.8 | 9.6 | 9.9 | 8.4 | 7.7 | 7.6 | 6.7 | 5.4 | 5.5 | ||
| Y | 7.4 | 7.6 | 8.3 | 8.6 | 9.4 | 9.3 | 9.5 | 9.5 | 9.4 | 8.4 | 7.5 | 8.5 |
Діапазон зміни X і Y розбиваємо на 5 інтервалів, так як 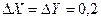. Інтервали (0;0.2) (0.2;0.4) (0.4;0.6) (0.6;0.8) (0.8;1).
2. Визначаємо за табл. 1 відносні частоти влучення X і Y в інтервали W(xi); W(yi), а також відносні частоти подій (xi, yi):W(xi, yi). Дані зводимо в табл. 2.
Таблиця 2
| Xi | ||||||
| Yi | x1 | x2 | x3 | x4 | X5 | W(yj) |
| y1 | 3/30 | 3/30 | ||||
| y2 | 2/30 | 3/30 | 1/30 | 6/30 | ||
| y3 | 1/30 | 1/30 | ||||
| y4 | 7/30 | 3/30 | 1/30 | 11/30 | ||
| y5 | 3/30 | 6/30 | 9/30 | |||
| W(xi) | 5/30 | 3/30 | 9/30 | 6/30 | 7/30 |
3. Оцінюємо ентропію повідомлень H(X),H(Y)
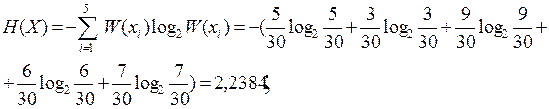
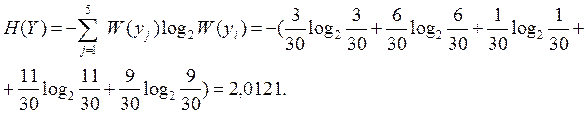
4. Визначаємо ентропію складного повідомлення H(x, y)
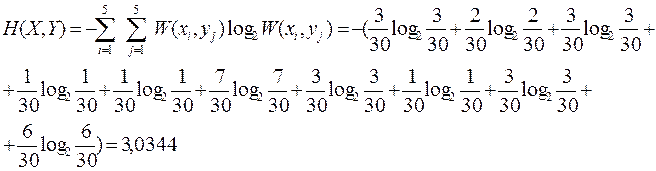
5. Обчислюємо умовні ентропії
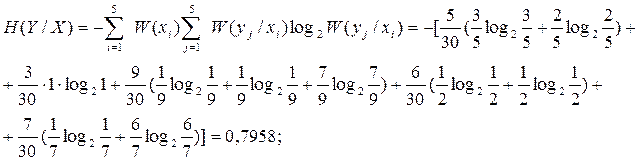
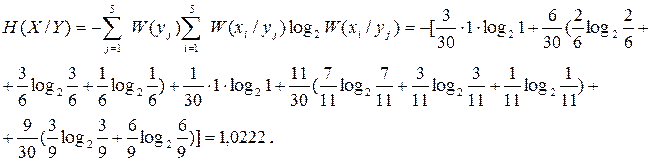
6. Виконуємо перевірку
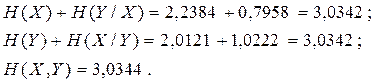
Точність розрахунків задовільна.
5. Завдання. Для заданих реалізацій X(t), Y(t) статистично залежних величин виконати інформаційний аналіз складного повідомлення (X, Y).
Date: 2015-05-22; view: 518; Нарушение авторских прав