
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторна робота 1
|
|
Міністерство освіти і науки України
Національний гірничий університет
Методичні вказівки
до виконання лабораторних робіт
з дисципліни
«Системний аналіз»
Дніпропетровськ
Міністерство освіти і науки України
Національний гірничий університет
Методичні вказівки
до виконання лабораторних робіт
з дисципліни
«Системний аналіз»
Рекомендовано до видання науково-
методичним управлінням університету
(протокол № від р.)
Дніпропетровськ
НГУ
Методичні вказівки до виконання лабораторних робіт з дисципліни “Системний аналіз”/ Уклад. І.В. Новицький, М.М. Одновол.- Дніпропетровськ: Національний гірничий університет, 2003.- 49 с.
Укладачі: І.В. Новицький, д-р техн. наук, проф.
М.М. Одновол, доцент.
Відповідальний за випуск завідувач кафедри системного аналізу і управління В.В. Слєсарєв, д-р техн. наук, проф.
Введення
Одним з основних етапів при проведенні системного аналізу є дослідження інформаційних потоків в об'єкті. Основний зміст цього етапу роботи складається, власне кажучи, в інформаційному аналізі і припускає розгляд досліджуваного об'єкта як інформаційної системи. Основою функціонування інформаційних систем є процеси передачі, перетворення і накопичення інформації. Відповідно критерієм якості роботи інформаційних систем є їхня здатність передавати, накопичувати чи перетворювати необхідну кількість інформації в одиницю часу при припустимих перекручуваннях і витратах. Дійсний посібник містить кілька типових задач інформаційного аналізу, що мають практичний додаток.
Лабораторна робота 1
Структурно-топологічний аналіз систем
При структурному аналізі в умовах мінімуму апріорної інформації про структуру системи враховується тільки факт наявності зв'язку між елементами і її спрямованість. Тому формалізація опису структур виконується за допомогою теорії графів.
Визначення графа. Нехай задана безліч елементів V. Граф G(V) вважається визначеним, якщо задане сімейство сполучень елементів чи пар вигляду E=(a,b), де a,b є V, що вказує які елементи вважаються зв'язаними. Пара E = (a,b) називається ребром, а елементи a,b – вершинами. Якщо порядок розташування кінців байдужний, то (a,b) - неорієнтоване ребро, якщо цей порядок важливий, то (a,b) – орієнтоване ребро чи дуга. Відповідно графи, що складаються з ребер, називають неорієнтованими (рис.1), а з дуг (рис.2) – орієнтованими.
Nbsp; Рис.1 Рис.2
Способи формалізованого завдання графа
Існує три способи завдання графа.
1.Графічний. Найбільш наочний спосіб, однак він не може бути використаний при розв’язанні задачі на ЕОМ.
2.Матричний. Матриця суміжності для неорієнтованого графа має вигляд:
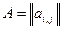 , де
, де
- 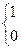 - при наявності зв'язку між вершинами i,j;
- при наявності зв'язку між вершинами i,j;
- - при відсутності зв'язку.
Для графа (рис.1)
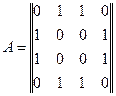
Для орієнтованого графа елементи ai,j визначаються так:
- 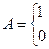 -якщо з i можливо перейти в j;
-якщо з i можливо перейти в j;
- -у противному випадку.
Для графа (рис.2)
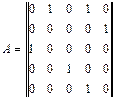 |
Якщо занумерувати ребра графа, то його можливо задати матрицею інцидентності
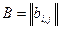 ;
; 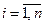 ;
; 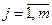 ,
,
де n – число вершин, m – число ребер.
Для неорієнтованого графа
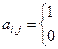 - якщо i-а вершина інцидентна j-му ребру;
- якщо i-а вершина інцидентна j-му ребру;
- якщо немає зв'язку.
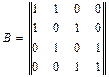 |
Для графа (рис.1)
Для орієнтованого графа
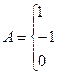 -якщо i- а вершина є початком j-го ребра;
-якщо i- а вершина є початком j-го ребра;
-якщо і- а вершина є кінцем j-го ребра;
-якщо зв'язку немає.
Для графа (рис.2)
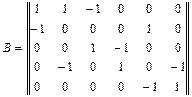 |
3.Множинний. Для графа G(V) задається безліч вершин V і відповідність G, що показує, як вони між собою зв'язані. Відповідність G(i) показує безліч вершин, у які можливо потрапити з i. Для графа (рис.2): G(1)=(2,4); G(2)=(5); G(3)=(1); G(4)=(3); G(5)=(4).
Можливо задати відповідність G-1(j), що визначає безліч вершин, з яких можливо потрапити в i.
Для графа (рис.2)
G-1(1)=(3);G-1(2)=(1);G-1(3)=(4);G-1(4)=(1,5);G-1(5)=(2).
Основні характеристики графа
Ланцюгом називається послідовність ребер E1,E2...En, коли кожне з ребер Еі стикається одним із кінців з ребром Ei+1. Ланцюг можна позначити послідовністю вершин, що вона містить.
Шляхом називається послідовність дуг, коли кінець попередньої дуги збігається з початком наступної.
Довжиною ланцюга (шляху) називають число ребер (дуг), що входять у ланцюг (шлях).
Матриця суміжності вершин А є матрицею матриці А:Аk = Ak-1 *A.
Елемент матриці Ak a(k)i,j визначає число шляхів довжиною k від вершини i до j, безпосередніх шляхів графа, що мають довжину, рівну одиниці. Загальне число транзитних шляхів від вершини і до вершини j довжиною K виходить шляхом піднесення до степеня К.
Число ребер, інцидентних вершині неорієнтованого графа, називають ступенем вершини P(i).
Структурно – топологічні характеристики систем
Основні структурні характеристики систем можна кількісно оцінити, використовуючи їхньої моделі у вигляді графів. Розглянемо основні структурні характеристики систем.
1.Зв’язність структури. Ця характеристика дозволяє виявити наявність обривів у структурі, (висячі вершини).
Для орієнтованого графа зв’язність елементів визначається матрицею зв’язності З, де
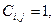 якщо
якщо 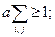
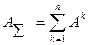 ; (1)
; (1)
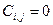 якщо
якщо 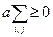 .
.
Для неорієнтованого графа зв’язність усіх елементів відповідає виконанню умови
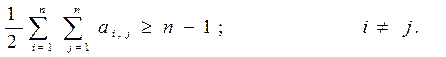
(2)
2.Структурна надмірність – це параметр, що показує перевищення загального числа зв'язків над мінімально необхідним. Визначається в такий спосіб:
для системи з мінімальною надмірністю R=0; для незв'язних систем R може бути негативним.
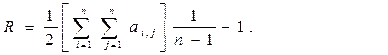
(3)
3.Рівномірність розподілу зв'язків у структурі неорієнтованого графа, що має m ребер і n вершин характеризується показником
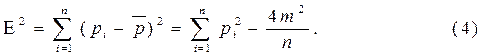 |
Показник Е2 характеризує недовикористання можливостей структури, що задана.
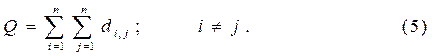 |
4.Структурна компактність – це параметр, що показує близькість елементів між собою:
di,j– мінімальна довжина ланцюга між вершинами i і j.
 |
Часто структурна компактність характеризується відносним показником
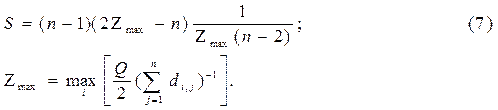 |
5.Ступінь централізації в структурі характеризується індексом центральності.
Індекс центральності змінюється в діапазоні від 0 до 1.
6.Ранг елемента дозволяє розподілити елементи системи в порядку їхньої значимості. Значимість елемента визначається числом його зв'язків з іншими елементами. Ранг елемента використовується при представленні структури системи у вигляді орієнтованого графа і може бути обчислений за формулою:
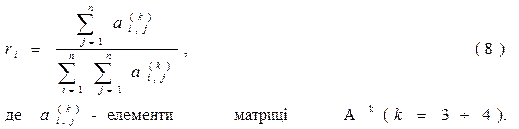
Приклад 1. Система задана наступною структурною схемою (рис.3). Розрахувати її структурно – топологічні характеристики і порівняти їх з характеристиками типу “кільцева” (рис.4).
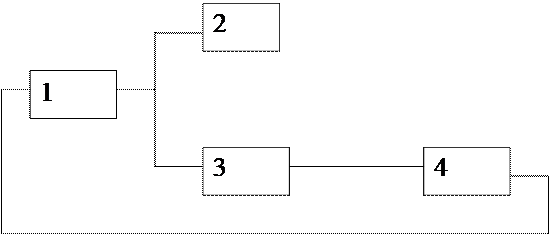 |
Рис.3. Структурна схема системи

а) 1 2 3 4 5
послідовна;
б) 1 2
5 4
кільцева;
 в) 2
в) 2
4 1 3
радіальна;
 г) 1
г) 1
2 3
4 5
деревоподібна;

д) 1
2 5
3 4
повний граф
Рис.4. Типові види структур для n=5.
Спочатку вихідну структурну схему (рис.3) представимо у вигляді неорієнтованого графа (рис.5).

 2
2

 |

1 
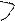
 4
4
 | |||
 | |||

Рис.5
Типова кільцева структура для n=4 відповідає графу рис.6.

1 3
Рис.6
Обчислимо структурно-топологічні характеристики графів (рис.5 і Рис.6) і порівняємо їх між собою.
Зв’язність структури
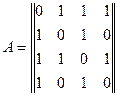 |
Для графа (рис.5) складемо матрицю суміжності
Перевіримо умову (2).
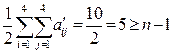
|
- умова зв’язності виконується.
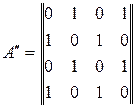 |
Аналогічно для графа (рис.6)
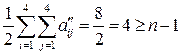
|
- умова зв’язності виконується.
Структурна надмірність (розраховується за (3)).
Для графа (рис.5)
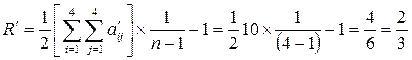 . .
|
Для кільцевої структури
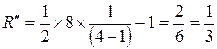 .
.
Висновок: структура (рис.3) має в два рази більшу надмірність в порівнянні з кільцевою.
Рівномірність розподілу зв'язків. (розраховується за (4)).
Для графа (рис.5)
m=5 – число ребер;
n=4 – число вершин.
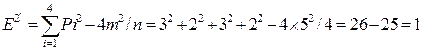
;
p1=3; p2=2; p3=3; р4=2.
Для графа (рис.6)
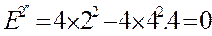 |
;
m=5;
n=4;
p1=p2=p3=p4=2.
У графі (рис.6) зв'язки розподіляються більш рівномірно.
Структурна компактність. Оцінимо її оптимальним показником за(6).
Для графа рис.5:d12=d13=d14=1;
d21=d23=1; d24=2;
d31=d32=d34=1;
d41=d43=1; d42=2.
Тоді
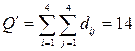 ;
;
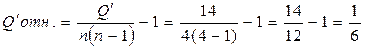 |
.
Аналогічно, для графа (рис.6)
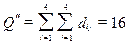 d12=d14=1; d13=2;
d12=d14=1; d13=2;
; d21=d23=1; d24=2;
d32=d34=1; d31=2;
d41=d43=1; d42=2.
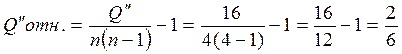 |
.
Ступінь централізації в структурі оцінимо за індексом центральності (7).
Для графа (рис.5)
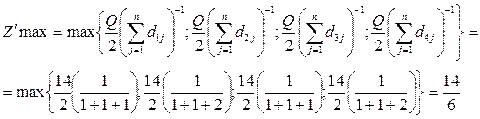 |
;
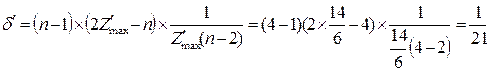 |
.
Для графа (рис.6)
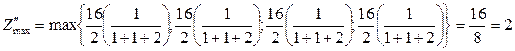 |
;
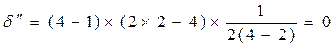 |
.
Структура (рис.5) має малий степінь централізації, структура (рис.6) абсолютно децентралізована.
Приклад 2. Дано структурну схему системи (рис.7.). Ранжирувати її елементи в порядку їхньої структурної значимості.

1 2 4
Рис.7
Представимо систему (рис.7) у вигляді орієнтованого графа (рис.8).

 1 3
1 3
Рис.8
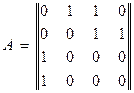
|
Матриця суміжності графа (рис.8) має вигляд:
Для розрахунку рангів елементів системи обчислимо матрицю A4
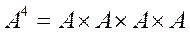 .
.
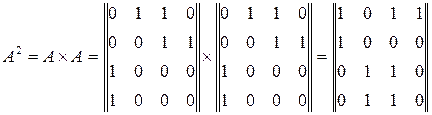
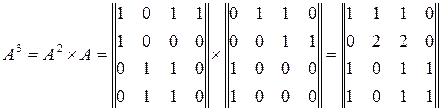
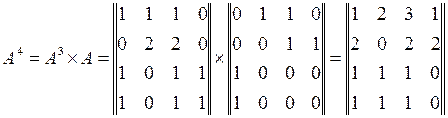
|
Обчислимо
Обчислимо ранги елементів системи (рис.7) за формулою (8).
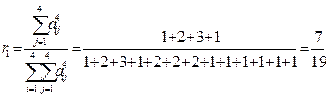 |
;;
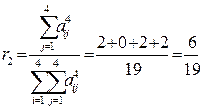 |
;
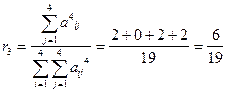 |
;
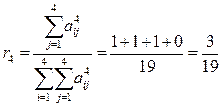 |
.
Елементи системи в порядку їхньої структурної значимості розташовуються в такий спосіб:



1 2 3і4
Завдання 1. Розрахувати структурно-топологічні характеристики даної викладачем системи і порівняти їх з характеристиками однієї з типових структур.
Завдання 2. Ранжирувати елементи даної викладачем системи в порядку їхньої структурної значимості.
Date: 2015-05-22; view: 1046; Нарушение авторских прав