
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приклад. Одержати послідовність чисел {yi}, що мають показовий розподіл
|
|
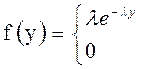 ;
; 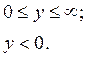
Відповідно до (2)маємо
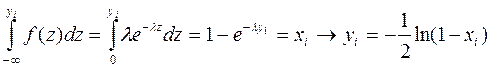 .
.
У деяких випадках рівняння (2) аналітично розв`язати важко. У цьому випадку або застосовуються числові методи його розв`язку або емпіричні формули. Наприклад, величина u нормально розподілена і має параметри.

При розрахунках 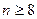 .
.
Для одержання нормальної послідовності з параметрами  досить виконати лінійне перетворення
досить виконати лінійне перетворення

Визначення обсягу обчислювальних експериментів
Припустимо, що необхідно визначити число експериментів N для оцінки деякого показника ефективності E, що є функцією параметрів системи чи алгоритму структури. Для цього використовують формулу

де  – точність оцінки;
– точність оцінки; 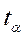 – аргумент нормального закону розподілу, що відповідає заданій надійній імовірності
– аргумент нормального закону розподілу, що відповідає заданій надійній імовірності 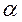 і визначається за таблицями Лапласа, тобто
і визначається за таблицями Лапласа, тобто
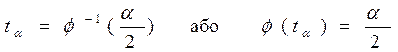 .
.
Часто середнє квадратичне відхилення 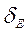 невідоме.
невідоме.
Тому попередньо проводиться серія обчислювальних експериментів, у ході яких оцінюється 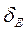 , а потім обчислюється необхідний обсяг експерименту за (5).
, а потім обчислюється необхідний обсяг експерименту за (5).
Методика розрахунку наступних станів типових динамічних ланок
Інтегруюча ланка
 X W(p) Y
X W(p) Y 
З урахуванням дискретного характеру часу, похідну представимо у вигляді відношення приростів
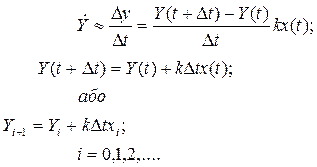
Перед початком розрахунків Y(0) повинне бути задано.
2. Диференціальна ланка
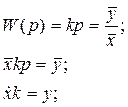
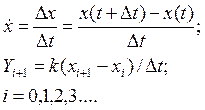
Перед початком розрахунків X(0) повинне бути задано.
3.Аперіодична ланка
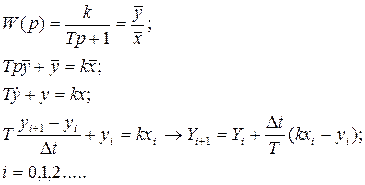
Перед початком розрахунків Y(0) повинне бути задано.
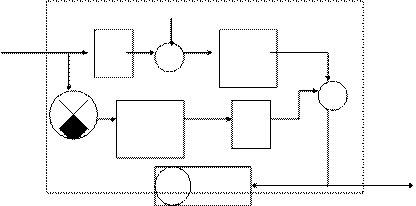
Приклад. Дано систему автоматичного керування у вигляді структурної схеми (рис.1) Тут позначено
 Х F
Х F
Н.Э Х 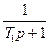 Х- вхід системи;
Х- вхід системи;
Х У- вихід системи;
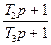
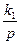 F- що обурює;
F- що обурює;
У- вплив;
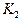 P
P
Н.Э.- нелінійний елемент.
Рис.1
Вихідні дані
Значення параметрів структурної схеми
Т1=2; Т2=1; Т3=0,5; ДО1=0,5; ДО2=2.
Залежність виходу нелінійного елемента від входу
Хвых=Х2вх.
Закон зміни вихідної змінної
 .
.
4.Крок квантування незалежної змінної t за часом при машинній імітації 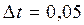 .
.
5.Закон розподілу випадкової величини F. F розподілена за нормальним законом з математичним чеканням 0,4 і середнім квадратичним відхиленням 0,3.
6.Початкові стани інерційних ланок. Усі виходи інерційних ланок у момент t=0 дорівнюють нулю.
Потрібно методом 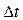 розрахувати процес зміни виходу системи у(t) на інтервалі
розрахувати процес зміни виходу системи у(t) на інтервалі 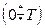 Т=3.
Т=3.
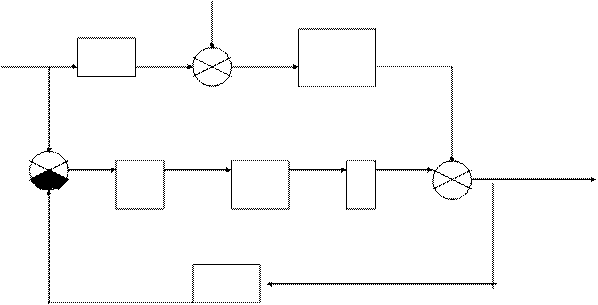
Спочатку перетворимо структурну схему системи і введемо проміжні змінні (рис.2).
 F
F
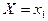 Н.Э
Н.Э 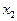
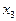
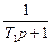
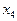
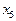

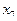
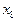
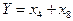
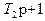
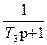
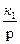
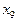
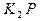
Рис.2
Основні співвідношення між змінними мають вигляд:
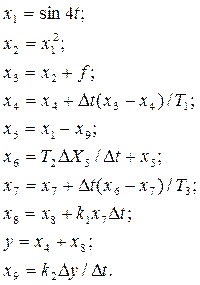
Для визначення кількості розрахункових вузлів заданий часовий інтервал 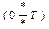 розділимо на крок квантування за часом
розділимо на крок квантування за часом 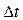
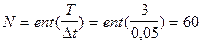 .
.
Порядок розрахунку змінних Х в обчислювальному алгоритмі повинний бути таким, щоб на черговому i-ом кроці праві частини розрахункових співвідношень були визначені. З врахуванням цього обчислювальний алгоритм має вигляд
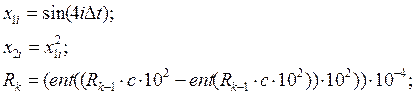
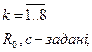
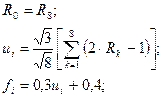
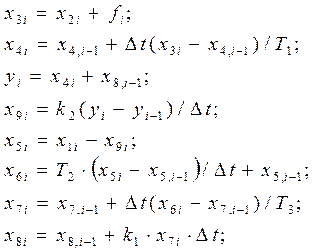
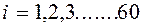 .
.
Перед початком розрахунків необхідно задати 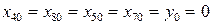 (відповідно до п.6 завдання).
(відповідно до п.6 завдання).
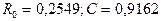 - довільні числа для генератора випадкової послідовності
- довільні числа для генератора випадкової послідовності 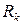 .
.
Перший крок обчислень для i=1 (момент часу 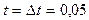 ) має вигляд
) має вигляд
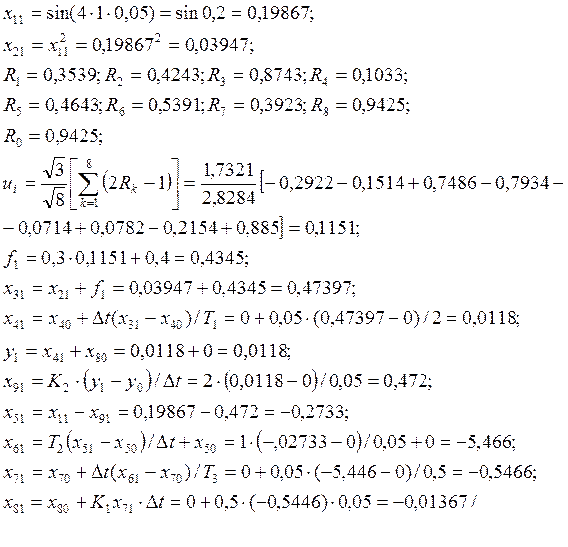
і т.д. для i від 2 до 60.
Завдання. Для заданої структурної схеми і її параметрів методом 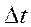 розрахувати процес зміни виходу системи y(t) на інтервалі
розрахувати процес зміни виходу системи y(t) на інтервалі 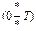 .
.
З використанням ЕОМ виконати дослідження залежність 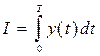 від заданого (обведеного кружечками) параметра системи при зміні цього параметра на 20% в обидва боки від заданого значення.
від заданого (обведеного кружечками) параметра системи при зміні цього параметра на 20% в обидва боки від заданого значення.
Лабораторна робота 4
Розрахунок характеристик моделей масового обслуговування
Марковський процес типу “загибель і розмноження” може бути використаний як модель великої кількості реальних процесів для аналізу їхніх показників ефективності функціонування. У граничному стаціонарному режимі такий процес характеризується ймовірностями станів, що визначаються за формулами
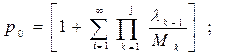 |
(1)
 |
(2)
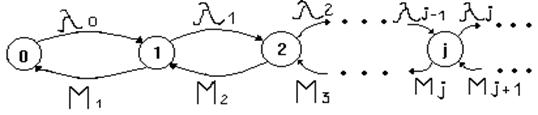 |
При цьому граф станів процесу має вигляд
Тут λj, Μj - інтенсивності переходів для ј-го стану. Існує декілька типових систем масового обслуговування, описуваних процесами ” загибель і розмноження”, для яких загальні вирази (1),(2) конкретизуються.
1. Системи без затрат з необмеженим чеканням і джерелом з нескінченним числом вимог
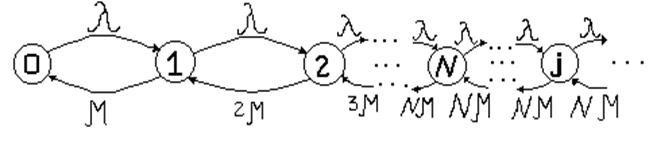
Передбачається, що система містить N однакових обслуговуючих каналів з однаковою інтенсивністю обслуговування
j – число вимог у системі;
λj = λ;
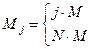 при
при 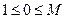 ;
;
при 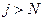 .
.
На основі формул (1),(2) отримаємо вирази для розрахунку ймовірностей станів
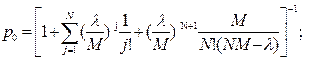 |
(3)
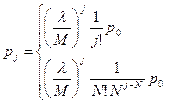
при 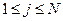 ;
;
(4)
при 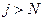 .
.
Існування кінцевої середньої черги в системі можливе при виконанні умови
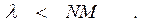 (5)
(5)
У цьому випадку показники ефективності системи розраховуються за формулами
1.Імовірність простою системи –P0.
2.Середнє число вимог у черзі
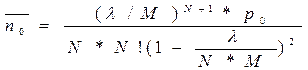 .
.
3.Середнє число зайнятих каналів
 .
.
4.Середнє число вимог у системі
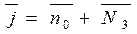 . (6)
. (6)
5.Середній час чекання вимоги в черзі
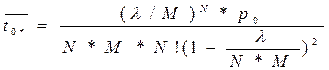 .
.
6. Середній час перебування вимоги в системі
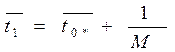 .
.
2. Системи без затрат із джерелом чисельності вимог.
У подібних системах інтенсивність потоку вимог, що надходять, залежить від стану системи, оскільки загальне число вимог у системі залишається постійним.
Вважаємо, що система має N каналів з інтенсивністю обслуговування М для кожного каналу і джерело, що містить постійну чисельність m вимог, що надходять з інтенсивністю λ для кожної вимоги, причому m>N.
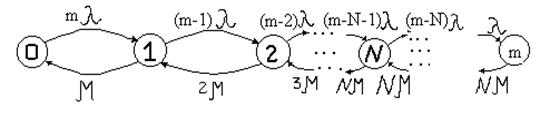 |
Граф станів системи має вигляд
Інтенсивність переходів у графі визначається в такий спосіб:
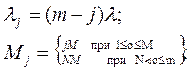
З урахуванням виразів для λj, Мj на основі (1),(2) формули для розрахунку ймовірностей станів мають вигляд
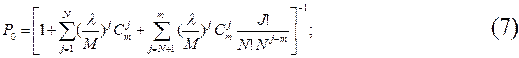
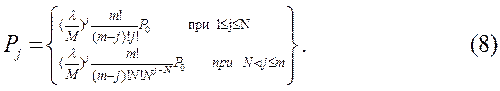
Показники ефективності системи розраховуються за формулами:
1.Імовірність простою системи -Р0.
2.Середнє число вимог у черзі
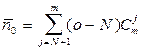 .
.
3. Середнє число зайнятих каналів
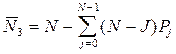 .
.
4. Середнє число вимог у системі (9)
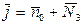 .
.
5. Середній час чекання вимоги в черзі
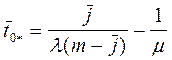 .
.
6. Середній час перебування вимоги в системі
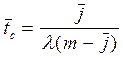 .
.
Приклад 1. На дробильно-перевантажувальний комплекс у середньому за 8 годин надходить 200 самоскидів із щебенем. Комплекс включає 3 розвантажувальних пункти. У середньому розвантаження самоскида займає 4 хвилини. Потрібно визначити основні характеристики цього об'єкта як системи масового обслуговування, якщо потік самоскидів можливо вважати найпростішим, а час розвантаження має експонентний розподіл.
Даний об'єкт може розглядатися як система масового обслуговування без втрат і джерелом із нескінченною чисельністю вимог. Визначимо її параметри.
Число каналів обслуговування дорівнює трьом (три розвантажувальних пункти), тобто N=3.
Інтенсивність вихідного потоку вимог (потік самоскидів) 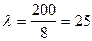 годин-1.
годин-1.
Інтенсивність обслуговування одного каналу
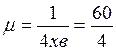 год-1=15 год-1.
год-1=15 год-1.
Граф станів системи
l l l l l l
 |  |
0 1 2 3...... j......
 |  |  |  |  | |||||||
 |

m 2m 3m 3m 3m 3m
Оскільки умова (5) виконується l<3m, то за формулою (3) обчислюємо ймовірність простою системи 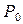
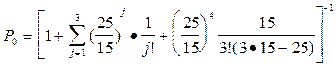 .
.
Потім за формулою (6) розраховуються показники ефективності системи.
Приклад2. 6 абонентів працюють із двома інформаційними центрами. На протязі однієї години кожен абонент у середньому звертається із запитом на обслуговування 10 разів. Обслуговування одного абонента в середньому продовжується 3 хвилини. Якщо обидва центри на момент запиту зайняті, то абонент переходить на режим чекання. Визначити показники ефективності такого об'єкта як системи масового обслуговування, якщо потік запитів можливо вважати найпростішим, а час обслуговування підкоряється експонентному закону розподілу.
Оскільки абонент, що обслуговується, чи абонент, що знаходиться в режимі чекання, надіслати новий запит не може, а численність абонементів кінцеве, то даний об'єкт може розглядатися як система без витрат з джерелом кінцевої численності вимог. Визначимо її параметри.
Численність каналів обслуговування дорівнює двом, тобто N=2.
Постійна численність вимог у системі дорівнює шести, тобто m=6.
Інтенсивність однієї вимоги (інтенсивність потоку заявок одного абонента) l=10 год-1.
Інтенсивність обслуговування одного каналу
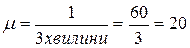 год-1.
год-1.
Граф станів системи має вигляд:
6l 5l 4l 3l 2l l
 |
0 1 2 3 4 5 6
 |  |  |  |  |  |
l 2l 2l 2l 2l 2l
По формулі (9) розраховуються показники ефективності системи
Завдання1. На збагачувальній фабриці ділянка КВП і А обслуговує А одиниць устаткування. У середньому через В хвилин кожна одиниця устаткування вимагає обслуговування однією людиною на протязі С хвилин. Визначити мінімально необхідну кількість електрослюсарів на ділянці, щоб об'єкт, що потребує обслуговування, знаходився в цьому стані в середньому не більше Д хвилин?
А,Б,С,Д - задаються викладачем, причому Д>С. А, В, С, Д знаходяться в межах: 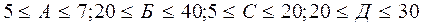 .
.
Завдання2. На базу матеріально-технічного постачання під навантаження надходить за 8-годинну зміну в середньому А автомобілів. Один навантажувач вантажить автомобіль у середньому В хвилин. Визначити мінімально необхідну кількість навантажувачів для того, щоб середнє число автомобілів у черзі під навантаження не перевищувало С штук.
А,В,С - задаються викладачем. Межі варіювання: 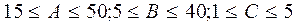 .
.
Лабораторна робота 5
Визначення кількості інформації в незалежних повідомленнях
1. Теоретичні відомості. Фундаментальним питанням для теорії інформації є питання про кількісну міру інформації. Відомо, що всяка інформація отримується споживачем після прийняття повідомлення, тобто в результаті досліду. Повідомлення, одержуване на прийомному боці, несе корисну інформацію лише в тому випадку, коли мається невизначеність щодо стану джерела повідомлення. Мірою невизначеності стану джерела (об'єкта) є ентропія. Якщо джерело може знаходитися в n станах 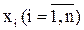 з імовірностями р(xi), то його ентропія визначається за формулою
з імовірностями р(xi), то його ентропія визначається за формулою
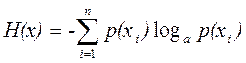 . (1)
. (1)
Кількість інформації, що міститься в повідомленні хi про стан джерела (об'єкта), якщо відомо, що він може знаходитися в одному з n станів з імовірністю р(xi)  визначається за такою ж формулою:
визначається за такою ж формулою:
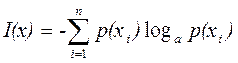 . (2)
. (2)
Незважаючи на збіг значень (1) і (2), ентропія Н(х) і кількість інформації I(x) є принципово різними поняттями. Н(х) є об'єктивною характеристикою джерела повідомлень і, якщо відома статистика повідомлень, може бути обчислена апріорно, тобто до одержання повідомлення. I(x) є апостеріорною характеристикою і визначає кількість інформації, одержувану з надходженням повідомлення.
Одиниці виміру I(x) і Н(х) залежать від вибору основи логарифма у формулах (1) і (2). При використанні двійкових логарифмів, що зручно при аналізі процесів в ЕОМ і інших пристроях, що працюють на базі двійкової системи числення, ентропія і кількість інформації виміряються в двійкових одиницях – бітах.
Ентропія (і кількість інформації) для неперервного повідомлення визначається за формулою:
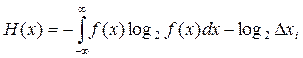 , (3)
, (3)
де f(x)- щільність розподілу ймовірностей неперервного повідомлення як випадкової величини; 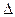 хi - крок квантування випадкової величини х, обумовлений точністю вимірювального приладу чи практичною доцільністю точності виміру ознаки х.
хi - крок квантування випадкової величини х, обумовлений точністю вимірювального приладу чи практичною доцільністю точності виміру ознаки х.
З практичної точки зору, для розрахунку ентропії неперервних повідомлень буває зручно користатися формулою
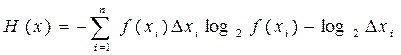 , (4)
, (4)
де 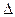 хi - крок квантування за змінною х; f(хi) – ордината
хi - крок квантування за змінною х; f(хi) – ордината
гістограми чи середня щільність розподілу f(x) на інтервалі 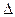 x.
x.
2.Постановка задачі. Диспетчер підприємства контролює m однотипних технологічних процесів за ознакою х(t), що змінюється в часі в деякому діапазоні xmin 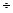 xmax.
xmax.
За заданою реалізацією х(t) визначити: чи буде встигати диспетчер вести контроль за m технологічними процесами, якщо відома (задана) необхідна точність виміру змінної х(t) - 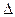 x і гранична максимальна швидкість сприйняття інформації людиною Imaх.
x і гранична максимальна швидкість сприйняття інформації людиною Imaх.
3.Методика рішення задачі
Вихідні дані
- реалізація контрольованого випадкового процесу х(t) на інтервалі 0 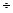 Т;
Т;
- необхідна точність контролю 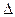 x;
x;
- гранична швидкість сприйняття інформації диспетчером – Iпред;
- кількість однотипних контрольованих процесів - m.
Етапи розрахунків
1.Формується масив дискретних відліків випадкового процесу xi 
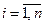 із кроком квантування за часом
із кроком квантування за часом 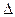 t, тобто
t, тобто 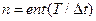 . Т - довжина реалізації.
. Т - довжина реалізації.
2.Будується автокорреляційна функція Rj випадкового процесу xi за формулою:
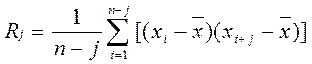 ,
, 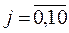 . (5)
. (5)
3.За графіком Rj визначається час спаду автокореляційної функції 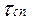
R(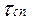 )=0.05R(0). (6)
)=0.05R(0). (6)
4.За часом спаду автокореляційної функції визначається періодичність контролю процесу х(t)
Tk= 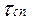 . (7)
. (7)
5.За дискретними відліками хi 
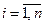 будується гістограма розподілу f(хi) випадкової величини Х з кроком
будується гістограма розподілу f(хi) випадкової величини Х з кроком 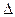 х.
х.
6.Визначається ентропія Н(х) і кількість інформації I(x), що містяться в одному вимірі
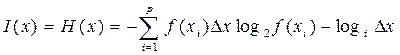 , (8)
, (8)
де Р- кількість інтервалів гістограми розподілу f(хi): р=ent[(xmax-xmin)/ 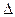 x]+1.
x]+1.
7. Розраховується необхідна швидкість сприйняття інформації диспетчером
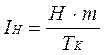 . (9)
. (9)
8. IH порівнюється з граничною швидкістю Iпред і робиться висновок про доцільність використання автоматизованих засобів контролю і переробки інформації.
Приклад. Вихідні дані.
Реалізація контрольованого випадкового процесу х(t) на інтервалі 0 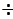 40c. Т=40 с.
40c. Т=40 с.
Необхідна точність контролю 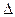 х=1.
х=1.
Гранична швидкість сприйняття інформації диспетчером Iпред=0.8 біт/с.
Кількість однотипних контрольованих об'єктів m=4.
На основі інформаційного аналізу даної системи обґрунтувати доцільність (недоцільність) застосування додаткових технічних засобів для контролю технологічного процесу.1.На основі реалізації х(t) формуємо масив дискретних відліків хi 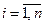 з кроком квантування за часом
з кроком квантування за часом 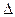 t=1, тобто n=40/1=40 (табл. 1).
t=1, тобто n=40/1=40 (табл. 1).
Таблиця 1
| I | хi | 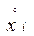
| i | хi | 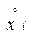
| i | хi | 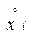
| I | хi | 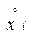
|
| 4.9 | -0.1 | 7.4 | 2.4 | 5.7 | 0.7 | 2.3 | -2.7 | ||||
| 5.6 | 0.6 | 8.3 | 3.3 | 5.6 | 0.6 | 4.1 | -0.9 | ||||
| 5.9 | 0.9 | 8.5 | 3.5 | 6.1 | 1.1 | 5.2 | 0.2 | ||||
| 5.3 | 0.3 | 6.6 | 1.6 | 5.8 | 0.8 | 5.6 | 0.6 | ||||
| 4.7 | -0.3 | 4.5 | -0.5 | 3.9 | -1.1 | 5.2 | 0.2 | ||||
| 4.9 | -0.1 | 3.9 | -1.1 | 2.9 | -2.1 | 4.9 | -0.1 | ||||
| 5.6 | 0.6 | 3.8 | -1.2 | 1.9 | -3.1 | 5.5 | 0.5 | ||||
| 6.5 | 1.5 | 4.9 | -0.1 | 1.4 | -3.6 | 6.0 | |||||
| 6.5 | 1.5 | 5.6 | 0.6 | 0.8 | -4.2 | 4.9 | -0.1 | ||||
| 6.7 | 1.7 | 5.9 | 0.9 | 1.3 | -3.7 | 4.9 | -0.1 |
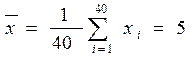 .
.
2.За даними таблиці 1 обчислюємо автокореляційну функцію процесу х(t) за формулою:
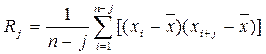 ,
, 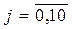
де 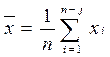 - середнє арифметичне випадкової величини х. Тоді
- середнє арифметичне випадкової величини х. Тоді
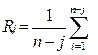
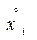
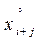 ,
, 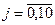
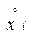 =
= 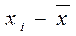 - центровані значення х (приведені в табл. 1).
- центровані значення х (приведені в табл. 1).
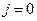 ;
;
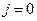
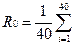
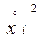 =
= 
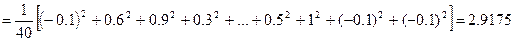 .
.
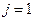 ;
; 
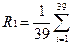
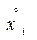
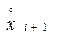 =
= 
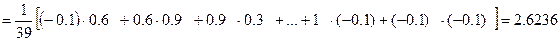 ;
;
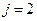 ;
; 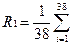
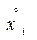
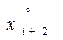 =
= 
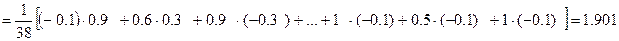 ;
;
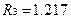 ;
; 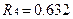 ;
; 
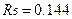 ;
; 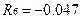 ;
; 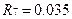 ;
;
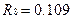 ;
; 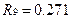 ;
;
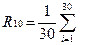
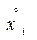
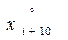 =
= 
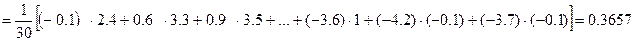 .
.
3.Будуємо графік автокореляційної функції Rj і визначаємо час спаду 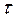 сп. Час спаду дорівнює 5 с.
сп. Час спаду дорівнює 5 с.
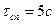
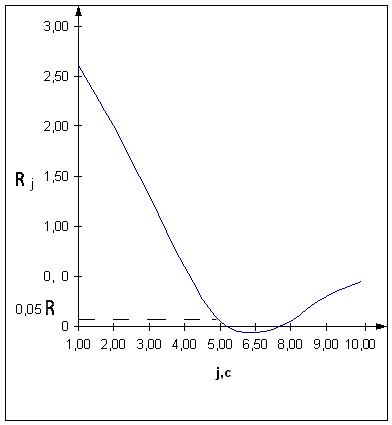
4.Приймаємо періодичність контролю процесу х(t) рівним часу спаду його автокореляційної функції, тобто
Тк= 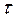 сп =5 с.
сп =5 с.
5.За дискретним відлікам xi 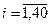 (табл. 1) будуємо гістограму відносних частот f(хi) із кроком
(табл. 1) будуємо гістограму відносних частот f(хi) із кроком 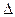 х=1 (табл. 2).
х=1 (табл. 2).
Табл. 2.
| Номер інтервалу | Інтервал | Частота влучення х інтервал | Відносна частота f(хi) |
| 0..1 | 1/40 | ||
| 1..2 | 3/40 | ||
| 2..3 | 2/40 | ||
| 3..4 | 3/40 | ||
| 4..5 | 9/40 | ||
| 5..6 | 13/40 | ||
| 6..7 | 6/40 | ||
| 7..8 | 1/40 | ||
| 8..9 | 2/40 |
6. Розраховуємо ентропію Н(х) і кількість інформації I(x), що
містяться в одному вимірі
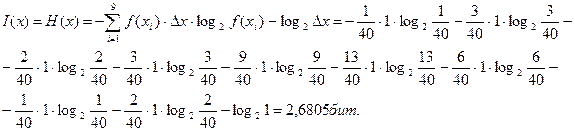
7. Розраховуємо необхідну швидкість сприйняття інформації диспетчером
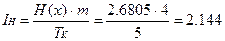 біт/з.
біт/з.
8.Тому що 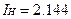 біт/з >
біт/з > 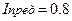 біт/з, то для контролю і керування чотирма(m=4) технологічними об'єктами необхідно використовувати автоматизовані засоби контролю і переробки інформації.
біт/з, то для контролю і керування чотирма(m=4) технологічними об'єктами необхідно використовувати автоматизовані засоби контролю і переробки інформації.
Завдання. На основі типової реалізації x(t) випадкового процесу при заданих точності контролю 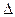 х, кількості об'єктів контролю m і граничній швидкості сприйняття інформації Iпред обґрунтувати доцільність застосування додаткових автоматизованих засобів переробки інформації на диспетчерському пункті.
х, кількості об'єктів контролю m і граничній швидкості сприйняття інформації Iпред обґрунтувати доцільність застосування додаткових автоматизованих засобів переробки інформації на диспетчерському пункті.
Date: 2015-05-22; view: 630; Нарушение авторских прав