Приведем несколько условий независимости

1. Независимость по разности. Предпочтения между двумя альтернативами, отличающимися лишь оценками по порядковой шкале одного критерия С₁ не зависят от одинако-вых оценок по другим критериям С₂,…,С_N. На первый взгляд, это условие кажется естественным и очевидным. Но возмож-ны случаи, когда оно не выполняется. Например: выбор авто-мобиля. При примерно одинаковой цене ЛПР предпочитает большую по размеру машину.

2. Независимость по полезности. Критерий C₁ называет-ся независимым по полезности от критериев С₂,…,C_N, если порядок предпочтений лотерей, в которых меняются лишь уровни критерия С₁ не зависит от фиксированных значений по другим критериям. Лотереей называется игра с двумя исходами: исходом х, получаемым с вероятностью р, и исходом у, получаемым с вероятностью 1-р.

Примером лотереи является подбрасывание монеты. При этом, как известно, с вероятностью р=0,5 выпадает орёл или решка. Пусть х = $10 и у = -$10 (т.е. мы получаем $10 при выпадении орла и платим столько же при выпадении решки). Ожидаемая (или средняя) цена лотереи определяется по формуле рх + (1 - р)у.

Как мы увидим далее, лотереи используются при пост-роении функций полезности по отдельным критериям.

3. Независимость по предпочтению является одним из наиболее важных и часто используемых условий.

Два критерия C₁ и С₂ независимы по предпочтению от других критериев С₃,…,C_N, если предпочтения между альтернатива-ми, различающимися лишь оценками по С₁, С₂, не зависят от фиксированных значений по другим критериям.

Приведем пример нарушения условия независимости по предпочтению — выбор дачи для летнего отдыха.

Критерий

Альтернатива Качество дачи Наличие магазина Расстояние

(комфорт) недалеко от дачи от города

А Хорошее Нет магазина

В Среднее Есть магазин

Вполне возможно, что альтернатива А предпочтитель-нее альтернативы В, если по критерию «Расстояние от города» оба варианта имеют оценку «Дача расположена недалеко от города».

В то же время, если оба варианта имеют по последнему критерию оценку «Дача расположена далеко от города», ва-риант В может оказаться предпочтительнее варианта А (то есть наличие магазина становится решающим).

ВЫВОД. Первые два условия независимости относи-лись к независимости одного критерия от остальных, тре-тье условие — к независимости пары критериев от прочих.

Если аксиомы первой группы и некоторые условия незави-симости выполнены, то из этого следует строгий вывод о су-ществовании многокритериальной функции полезности в оп-ределённом виде.

Приведём основную теорему многокритериальной тео-рии полезности, на которой основаны практические методы оценки альтернатив.

Если условия независимости по полезности и незави-симости по предпочтению выполнены, то функция поле-зности является аддитивной

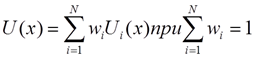
либо мультипликативной

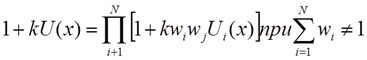
где U, U_i — функции полезности, изменяющиеся от 0 до 1;
w_i — коэффициенты важности (веса) критериев, причем 0 < w_i < 1; коэффициент k > -1.

Таким образом, многокритериальную функцию полезности можно определить, если известны значения коэффициентов w_i, к, а также однокритериальные функции полезности U_i(х).