Прямоугольный импульс

Аналитическое выражение: Временное представление:

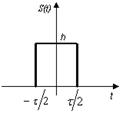
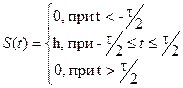
Рисунок 3.5 – Прямоугольный импульс

Для определения спектральной плотности амплитуд прямоугольного импульса воспользуемся интегралом Фурье (3.13) и формулой Эйлера (3.6)

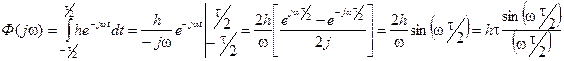(3.16)

Из (3.16) следует, что спектральная плотность амплитуды прямоугольного импульса описывается функцией вида 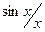. Из математики известно, что 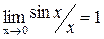. На рисунке 3.6 представлен график зависимости (3.16). Определим ширину спектра прямоугольного импульса ∆ω_пр, для чего определим значения частот, в которых наблюдается первый ноль, т.е. определим корни уравнения Ф(ω)=0. Выражение (3.16) обращается в ноль при значениях аргумента синуса кратных π: 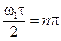, при n =±1.

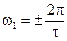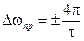Откуда и или 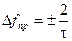. (3.17)

Из (3.17) следует, чем короче прямоугольный импульс, тем шире его спектр. В этом частном случае проявляется фундаментальное свойство преобразования Фурье: длительность сигнала и ширина его частотного спектра связаны обратно пропорциональной зависимостью.

Рисунок 3.6 – Амплитудный спектр прямоугольных импульсов

2) Дельта функция – δ(t) – это математическая (абстрактная) модель сигнала.

Аналитическое выражение

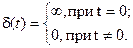
При этом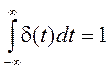

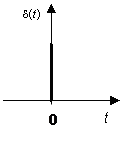
Рисунок 3.7 - Временное представление δ - функции

Спектральная плотность амплитуды: Ф(ω)=1. Дельта функция имеет сплошной бесконечно широкий спектр с постоянной спектральной плотностью.

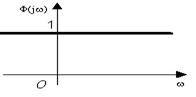
Рисунок 3.8 - Спектральное представление δ-функции

Date: 2015-05-22; view: 1812; Нарушение авторских прав