Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Частотный спектр периодического сигнала
|
|
Периодический сигнал S(t) изменяется непрерывно и имеет период Т0 повторения значений (рисунок 3.2). Такой сигнал может быть представлен бесконечной суммой гармонических колебаний:
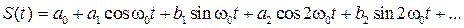(3.1)
Рисунок 3.2 - Периодический сигнал
В выражении (3.1) а0 представляет собой постоянную составляющую сигнала, принимающую среднее значение сигнала за период. Это может быть постоянный ток или постоянное напряжение. Затем следуют две составляющие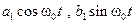 
с частотой:
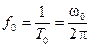. (3.2)
Эту частоту называют основной. Две следующих составляющих имеют частоту, равную удвоенной основной частоте, их называют вторыми гармониками. В общем случае ряд повторяется до бесконечности и частоты составляющих сигнала будут отличаться от основной частоты во все большее число раз, то есть появятся третья, четвертая и другие гармоники.
Приведенный ряд (3.1) можно представить в компактном виде:
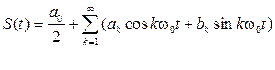, (3.3)
где k – номер гармонической составляющей, аk, bk – амплитуды k –гармоники. Такое разложение периодической функции времени называется рядом Фурье.
Амплитуды и начальные фазы любой гармоники определяются следующими выражении:
, 
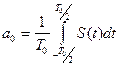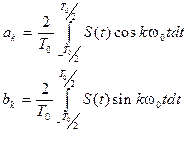; (3.4)
Если ввести такие характеристики как общую амплитуду и начальную фазу k – гармоник, то ряд Фурье можно записать в ви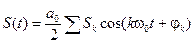де:
, где
,
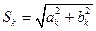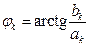. (3.5)
Не все физические величины можно оценить одним числом. Например, напряжение на участках цепи переменного тока одной частоты могут отличаться по амплитуде и по фазе, т.е. для характеристики каждого из них необходимо как минимум два числа a и b. Для этого используется комплексное представление сигнала.
Представим ряд Фурье в комплексной форме, заменяя тригонометрические функции показательными. Для замены тригонометрических функций показательными используются формулы Эйлера:
; 
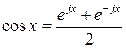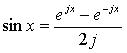, (3.6)
и обратные формулы Эйлера:
; 
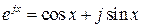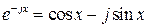. (3.7)
Подставив (3.6) в (3.3) и с учетом 1/j = –j, получим:
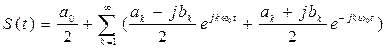(3.8)
Обозначим:
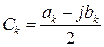
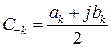. (3.9)
Тогда с учетом (3.4) и (3.7) составляющие амплитуды примут вид:
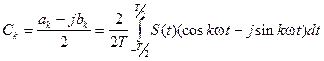
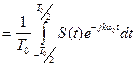. (3.10)
Аналогично: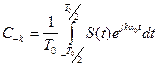 
. Заметим, что выражение для Ck отличается от C-k: лишь знаком перед мнимой частью. Вводя отрицательные значения k, с учетом (3.10) ряд Фурье (3.8) примет вид:
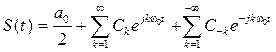(3.11)
В этом выражении присутствует среднее значение функции S(t) или постоянная составляющая сигнала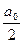 
. Используя выражение (3.4) для составляющих амплитуды, будем иметь:
.
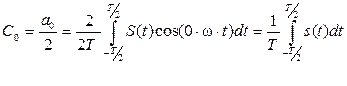Объединив обе суммы в выражении (3.11), получим комплексную форму записи ряда Фурье:
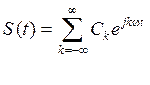, (3.12)
где Сk –комплексные амплитуды гармоник:
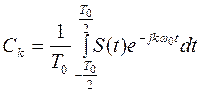(3.13)
Таким образом ряд Фурье показывает, что периодическая функция времени S(t) может быть представлена не только своими мгновенными значениями, но также и своими гармоническими составляющими c частотами, кратными основной частоте.
Пример представления периодического сигнала спектральными гармоническими составляющими представлен на рисунке 3.3:
| 
|
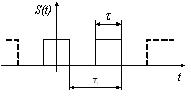
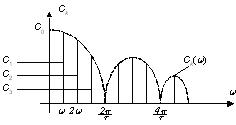
| Временное представление последовательности прямоугольных импульсов с периодом Т 0 | Спектральное представление функции, где 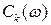 – огибающая модуля спектра последовательности прямоугольных импульсов.
|
Рисунок 3.3 – Частотный спектр периодического сигнала
Date: 2015-05-22; view: 1760; Нарушение авторских прав