
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прямоугольное (ортогональное) проецирование
|
|
Частный случай параллельного проецирования, при котором напраление проецирования перпендикулярно плоскости проекций (рис. 7)
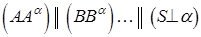
В дальнейшем безоговорочно используется ортогональное проецирование.
В ортогональном проецировании сохраняются все свойства параллельного проецирования. Кроме того, для ортогонального проецирования справедлива теорема о проецировании прямого угла (смотри тему №6) и применим способ определений расстояния между точками (т.е. длины отрезка, смотри тему №3), называемый способом прямоугольного треугольника.
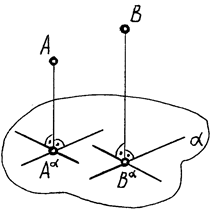
| Рис. 7 |
БОЛЕЕ ПОДРОБНО...
Положение предмета в пространстве определяют четыре его точки, не лежащие в одной плоскости. Изображение пространственного предмета на чертеже сводится к построению проекций множества точек этого предмета на плоскости R (называемой плоскостью проекций) при помощи прямых линий (проецирующих лучей), проходящих через точки предмета и направленных к центру проецирования S.
Однако, чтобы построить проекцию предмета, не обязательно строить все его точки. Достаточно найти лишь проекции характерных точек (вершин, ребер и т.п.), которые затем соединить соответствующей линией.
Проецирующие лучи в совокупности образуют проецирующую поверхность. Так, при проецировании прямой АВ проецирующей поверхностью является плоскость АВ ba (рис.).
Линия пересечения ab проецирующей плоскости с плоскостью R представляет собой проекцию прямой AB, которая слагается из проекций отдельных ее точек.
Проекция подобна тени, отброшенной от предмета, освещенного лампой или солнцем.
При проецировании кривой линии в первом случае проецирующие лучи образуют коническую поверхность с вершиной в точке S, получается к оническое (перспективное) изображение кривой (рис. 2). Во втором случае конус проецирующих лучей превращается в цилиндр и коническое изображение переходит вцилиндрическое (параллельное) (рис. 2). Проекция кривой линии рассматривается при этом как линия пересечения проецирующей поверхности с плоскостью R.
В перспективе предмет изображается таким, каким он представляется глазу наблюдателя. Хрусталик глаза является центром проецирования. Каждому из нас знакомо следующее явление: если смотреть вдоль полотна железной дороги, нам кажется, что рельсы как бы сближаются между собой и на горизонте сходятся в одну точку (центр), а опоры, расположенные вдоль путей, уменьшаются по мере удаления.
Параллельное проецирование — частный случай перспективы. Суть параллельного проецирования заключается в следующем: если условно удалить центр проецирования в бесконечность, то проецирующие лучи можно считать параллельными.
Так, чтобы построить параллельную проекцию треугольника ABC (рис.), нужно задать: R — плоскость проекций (не параллельную и не совпадающую с направлением проецирующих лучей); S — направление проецирующих лучей (направление проецирования).
Далее, через характерные точки предмета проводят проецирующие лучи Аа, Вb и Сс параллельно направлению проецирования, а затем находят точки a, b и с их пересечения с плоскостью R. Эти точки — искомые параллельные проекции точек А, В и С заданного треугольника.
Проекция abc — линия пересечения проецирующей призматической поверхности с плоскостью R. Форма и размеры параллельной проекции какого-либо предмета при заданном направлении проецирования зависят только от выбора направления плоскости проекций и не зависят от ее удаления от предмета. Треугольник, расположенный в плоскости R 1, параллельной плоскости проекций, проецируется равным заданному. В этом случае ab = AB, bc = BC, ac = AC.
В зависимости от угла наклона проецирующего луча к плоскости проекций параллельное проецирование делится на два вида: прямоугольное и косоугольное.
ПРЯМОУГОЛЬНЫМ (или ортогональным) проецирование называется в том случае, когда направление проецирования выбрано перпендикулярным плоскости проекций. В другом случае оно называется КОСОУГОЛЬНЫМ.
При прямоугольном проецировании (рис. 7) величина коэффициента искажения не может превышать единицы.
В косоугольных проекциях (рис. 5) коэффициент искажения (К = ab / AB) данного отрезка АВ может принимать любые числовые значения в зависимости от наклона отрезка и проецирующих лучей к плоскости проекций. В частности, если направление отрезка совпадает с направлением проецирования, то проекцией этого отрезка будет точка, а коэффициент искажения равен нулю.
В параллельном проецировании сохраняются основные свойства перспективы, а именно:
1) проекция точки есть точка;
2) проекция прямой в общем случае будет прямая;
3) каждой точке, принадлежащей какой-либо линии, соответствует проекция этой точки на проекции данной линии.
Кроме того, параллельное проецирование имеет еще ряд (только ему присущих) свойств:
4) если точка лежит на отрезке прямой, то проекция этой точки делит проекцию отрезка в том же отношении, в каком
точка делит отрезок, т.е. AC / CB = ас / cb (рис. 5);
5) проекцией пересекающихся отрезков будут также пересекающиеся отрезки, а точка их пересечения будет проекцией точки пересечения данных отрезков (рис. 3);
6) проекции параллельных отрезков параллельны, одного направления, а их отношение равно отношению длин отрезков, т.е. ab çç cd и AB / CD = ab / cd (рис. 4);
7) при прямоугольном проецировании прямой угол проецируется прямым углом только в том случае, если одна из его сторон параллельна плоскости проекций, а вторая не является проецирующим лучом (теорема о проецировании прямого угла).
Date: 2015-04-23; view: 812; Нарушение авторских прав